Các bài toán về cực trị hình học Cực trị hình học lớp 9
Các bài toán về cực trị hình học
GiaiToan.com biên soạn và đăng tải tài liệu Chuyên đề cực trị giúp học sinh hiểu rõ về cực trị và cách giải các bài toán về cực trị Toán lớp 9 nhanh và chính xác nhất. Chi tiết mời các em học sinh cùng tham khảo. Chúc các bạn học tập tốt!
1. Cực trị là gì?
Cách giải:
a) Khi tìm vị trí của hình H trên miền D sao cho biểu thức f có giá trị lớn nhất ta phải chứng tỏ được:
+ Với mọi vị trí của hình H trên miền D thì ![]() ( m là hằng số)
( m là hằng số)
+ Xác định vị trí của hình H trên miền D sao cho ![]()
b) Khi tìm vị trí của hình H trên miền D sao cho biểu thức f có giá trị nhỏ nhất ta phải chứng tỏ được:
+ Với mọi vị trí của hình H trên miền D thì ![]() ( m là hằng số)
( m là hằng số)
+ Xác định vị trí của hình H trên miền D sao cho ![]()
I. Bài tập vận dụng
Cho nửa đường tròn đường kính BC = 2 R. Từ điểm A trên nửa đường tròn vẽ ![]() . Nửa đường tròn đường kính BH, CH lần lượt có tâm O1, O2 cắt AB, AC theo thứ tự tại D và E
. Nửa đường tròn đường kính BH, CH lần lượt có tâm O1, O2 cắt AB, AC theo thứ tự tại D và E
a) Chứng minh tứ giác ADHE là hình chữ nhật, từ đó tính DE biết R = 25 và BH = 10
b) Chứng minh tứ giác BDCE nội tiếp đường tròn
c) Xác định vị trí điểm A đến diện tích từ giác DEO1O2 đạt GTLN. Tính giá trị đó.
Hướng dẫn giải
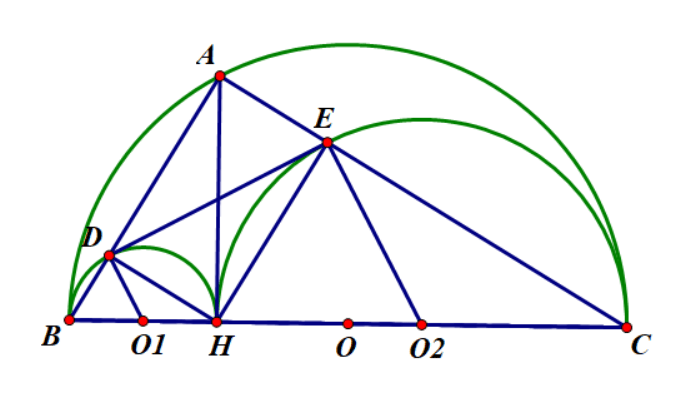
Ta có![]() ( vì góc nội tiếp chắn nửa đường tròn)
( vì góc nội tiếp chắn nửa đường tròn)
Tương tự ta có ![]()
Xét tứ giác ADHE có ![]() là hình chữ nhật nên DE = AH
là hình chữ nhật nên DE = AH
Mà ![]() ( hệ thức lượng trong tam giác )
( hệ thức lượng trong tam giác )
![]()
b) Ta có ![]()
Mà ![]()
![]()
Lại có ![]()
Tứ giác BDEC nội tiếp đường tròn
c) Ta có ![]() cân tại O1
cân tại O1 ![]()
Từ (1) và (2) ![]()
Vây DEO2O1 là hình thang vuông tại D và E
Ta có ![]()
Dấu bằng xảy ra khi và chỉ khi ![]() là hình chữ nhật. Khi đó A là điểm chính giữa cung BC
là hình chữ nhật. Khi đó A là điểm chính giữa cung BC
Ví dụ 2: Cho đường tròn ( O) đường kính AB, d1, d2 là các đường thẳng lần lượt qua A, B và cùng vuông góc với đường thẳng AB M, N là các điểm lần lượt thuộc d1, d2 sao cho .
a) Chứng minh MN là tiếp tuyến của đường tròn (O)
b) Chứng minh AM.AN =
c) Xác định vị trí của M, N để diện tích tam giác MON đạt GTNN
Hướng dẫn giải
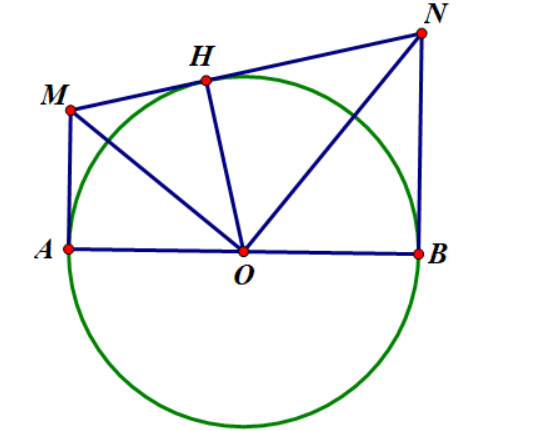
a) Gọi H là hình chiếu của O trên đường thẳng MN.
Xét tứ giác OAMH có: ![]() tứ giác OAMH nội tiếp đường tròn
tứ giác OAMH nội tiếp đường tròn
Tương tự ta có OANH nội tiếp đường tròn ![]() ( góc nội tiếp cùng chắn 1 cung)
( góc nội tiếp cùng chắn 1 cung)
![]() MN là tiếp tuyến
MN là tiếp tuyến
b) Ta có AM = MH, BN = NH, theo hệ thức lượng trong tam giác vuông, ta có:
![]() (đpcm)
(đpcm)
c) Ta có ![]() ( AMNB là hình thang vuông)
( AMNB là hình thang vuông)
Dấu “ =” xảy ra khi và chỉ khi MN = AB hay H là điểm chính giữa của cung AB hay MN// AB ![]()
Vậy khi và chỉ khi ![]()
----------------------------------------
Hy vọng tài liệu Cực trị sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết, bài tập Hàm số bậc nhất, từ đó vận dụng giải các bài toán Toán lớp 9 một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 9. Chúc các em học tốt.
- Lượt xem: 76





































