Bài 4 trang 29 Toán 10 tập 1 SGK Cánh Diều Giải Toán 10

1 Đánh giá

Bài 4 SGK Toán 10 trang 29

Toán 10 trang 29 Bài 4 là lời giải bài Hệ bất phương trình bậc nhất hai ẩn SGK Toán 10 Cánh Diều được GiaiToan.com biên soạn. Lời giải Toán 10 này với hướng dẫn chi tiết lời giải giúp cho các bạn học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán. Mời các bạn học sinh cùng tham khảo chi tiết.

Giải Bài 4 Toán 10 trang 29

Đề bài: Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất gấp hai lần thời gian làm ra một chiếc mũ kiểu thức hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thị tối đa trong một người là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.

Hướng dẫn:

Sử dụng hệ bất phương trình bậc nhất hai ẩn để giải bài toán.

Lời giải:

Gọi x, y lần lượt là số lượng chiếc mũ kiểu thứ nhất và kiểu thứ hai phân xưởng sản xuất được để tiền lãi thu được là cao nhất (chiếc, $x,y \in \mathbb{N}$ )

Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thị tối đa trong một người là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có:

$0 \leqslant x \leqslant 200,\,\,0 \leqslant y \leqslant 240$

Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Vậy tổng số tiền lãi khi bán mũ là $T = 24x + 15y$ (đồng)

Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Thời gian để sản xuất ra một chiếc mũ kiểu thứ hai là $\frac{1}{{60}}$ (giờ)

Thời gian để làm ra một chiếc mũ kiểu thứ nhất gấp hai lần thời gian làm ra một chiếc mũ kiểu thức hai. Vậy thời gian để sản xuất ra một chiếc mũ kiểu thứ nhất là $\frac{1}{{30}}$ (giờ)

Phân xưởng làm việc 8 tiếng mỗi ngày nên ta có bất phương trình:

$\frac{1}{{30}}x + \frac{1}{{60}}y \leqslant 8$

Bài toán đưa về: Tìm $x,y$ là nghiệm của hệ bất phương trình:

$\left\{ \begin{gathered} 0 \leqslant x \leqslant 200 \hfill \\ 0 \leqslant y \leqslant 240 \hfill \\ \frac{1}{{30}}x + \frac{1}{{60}}y \leqslant 8 \hfill \\ \end{gathered} \right.$ sao cho $T = 24x + 15y$ có giá trị lớn nhất.

Xác định miền nghiệm của hệ bất phương trình được:

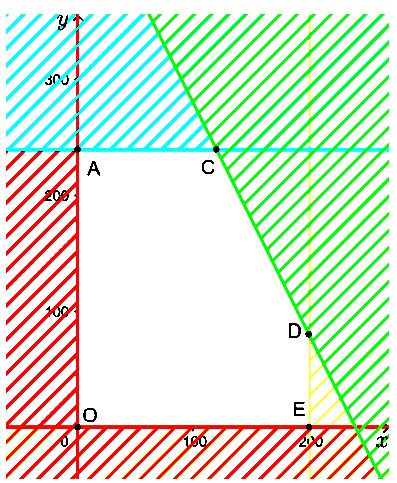
Bài 4 SGK Toán 10 trang 29

Miền nghiệm của hệ bất phương trình là ngũ giác $ACDEO$

Biểu thức $T = 24x + 15y$ có giá trị lớn nhất tại một trong các đỉnh của ngũ giác $ACDEO$ .

Thay tọa độ điểm $A\left( {0;240} \right)$ vào T có: $T = 24.0 + 15.240 = 3600$

Thay tọa độ điểm $C\left( {120;240} \right)$ vào T có: $T = 24.120 + 15.240 = 6480$

Thay tọa độ điểm $D\left( {200;80} \right)$ vào T có: $T = 24.200 + 15.80 = 6000$

Thay tọa độ điểm $E\left( {200;0} \right)$ vào T có: $T = 24.200 + 15.0 = 4800$

Thay tọa độ điểm $O\left( {0;0} \right)$ vào T có: $T = 24.00 + 15.0 = 0$

Vậy biểu thức $T = 24x + 15y$ có giá trị lớn nhất tại điểm $C\left( {120;240} \right)$ với $x = 120;\,\,y = 240$ .

Vậy để tiền lãi thu được là cao nhất, phân xưởng trong một ngày phải sản xuất 120 chiếc mũ kiểu thứ nhất và và 240 chiếc mũ kiểu thứ hai.

-----> Bài tiếp theo: Bài 1 trang 30 Toán 10 tập 1 SGK Cánh Diều

----------------

Trên đây là lời giải chi tiết Toán 10 trang 29 Bài 4 cho các bạn học sinh tham khảo, nắm được cách giải các dạng toán của Chương II: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn. Qua đó giúp các bạn học sinh ôn tập chuẩn bị cho các bài thi giữa học kì và cuối học kì lớp 10.

Chia sẻ bởi: