Bài 4.10 trang 54 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống Giải Toán 10 sách Kết nối tri thức

2 Đánh giá

Bài 4.10 trang 54 SGK Toán 10

Toán lớp 10 Bài 4.10 trang 54 là lời giải SGK Tổng và hiệu của hai vecto Toán 10 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 4.10 Toán 10 trang 54

Bài 4.10 (SGK trang 54): Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Bài 4.10 trang 54 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

Hướng dẫn giải

- Quy tắc ba điểm: Với ba điểm bất kì A, B, C ta có: $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}$

- Quy tắc hình bình hành: Nếu ABCD thì một hình bình hành thì $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

- Vecto có cùng độ dài và ngược hướng với vecto $\overrightarrow a$ được gọi là vecto đối của vecto $\overrightarrow a$

- Vecto đối của $\overrightarrow a$ được kí hiệu là $- \overrightarrow a$

- Vecto $\overrightarrow 0$ được coi là vecto đối của chính nó.

- Quy tắc hiệu: Với O, M, N ta có: $\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM}$

Lời giải chi tiết

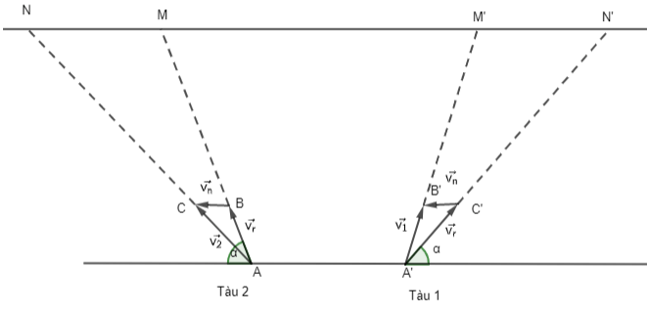
Ta biểu thị hai bờ sông là hai đường thẳng song song d₁, d₂ (H.4.17). Giả sử tàu 1 xuất phát từ A' ∈ d₁ và bánh lái luôn được giữ để tàu tạo với bờ một góc α. Gọi $\overrightarrow {{v_r}}$ và $\overrightarrow {{v_n}}$ lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi B’, C’ là các điểm sao cho $\overrightarrow {{v_r}} = \overrightarrow {A'C'} ;\overrightarrow {{v_n}} = \overrightarrow {C'B'}$

Khi đó tàu chuyển động với vận tốc thực tế là:

$\overrightarrow {{v_*}} = \overrightarrow {{v_r}} + \overrightarrow {{v_n}} = \overrightarrow {A'C'} + \overrightarrow {C'B'} = \overrightarrow {A'B'}$

Xét tam giác A’B’C’ ta có:

$\widehat {A'C'B'} = \alpha$ (So le trong)

${\left| {\overrightarrow {{v_*}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} - 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha$

Giả sử tàu 2 xuất phát từ A ∈ d₁ và bánh lái luôn được giữ để tàu tạo với bờ một góc α. Gọi $\overrightarrow {{v_r}}$ và $\overrightarrow {{v_n}}$ lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi B, C là các điểm sao cho $\overrightarrow {{v_r}} = \overrightarrow {AC} ;\overrightarrow {{v_n}} = \overrightarrow {CB}$

Khi đó tàu chuyển động với vecto vận tốc thực tế là:

$\overrightarrow {{v_1}} = \overrightarrow {{v_r}} + \overrightarrow {{v_n}} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB}$

Xét tam giác ABC có:

$\widehat {ABC} = {180^0} - \alpha$

$\begin{matrix} {\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} - 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \left( {{{180}^0} - \alpha } \right) \hfill \\ \Rightarrow {\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} + 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha \hfill \\ \end{matrix}$

Do 0⁰ < α < 90⁰ => cosα > 0

=> ${\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} + 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha > {\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} - 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha$

=> ${\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} + 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha > {\left| {\overrightarrow {{v_*}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} - 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha$

=> ${\left| {\overrightarrow {{v_1}} } \right|^2} > {\left| {\overrightarrow {{v_*}} } \right|^2}$

Vì độ dài hai quãng đường AN và A’M’ của tàu 2 và tàu 1 chênh nhau không đáng kể nên ta coi nó bằng nhau. Do đó vì vận tốc tàu 2 lớn hơn tàu 1 nên tàu 2 là tàu đi qua bờ bên kia trước.

------> Câu hỏi cùng bài:

----> Đây là câu hỏi trong bài: Giải Toán 10 Bài 8 Tổng và hiệu của hai vecto

----> Bài tiếp theo: Toán 7 Bài 9 Tích của một vecto với một số

----------------------------------------

Trên đây là lời giải chi tiết Bài 4.10 Toán lớp 10 trang 54 Tổng và hiệu của hai vecto cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 4: Vecto. Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10. Chúc các bạn học tốt!

Một số câu hỏi Toán lớp 10 đặc sắc mời bạn đọc tham khảo:

Chia sẻ bởi: