Bài 12 trang 89 Toán 8 Tập 1 sách Chân trời sáng tạo Bài tập cuối chương 3

Bài 12 trang 89 Toán 8 Tập 1 CTST

Bài 12 trang 89 Toán 8 CTST Tập 1 là lời giải chi tiết trong bài Bài tập cuối chương 3 SGK Toán 8 Chân trời sáng tạo tạo giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Giải Bài 12 trang 89 Toán 8 Tập 1

Lời giải chi tiết:

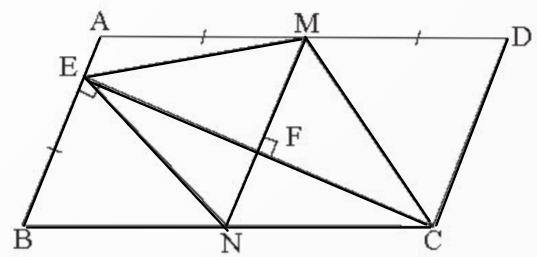
a) Ta có MN ⊥ CE (gt) và AB ⊥ CE (gt)

Suy ra MN // AB

Mà AB // CD (ABCD là hình bình hành) nên MN // CD

Xét tứ giác MNCD có MN // CD và MD // CN

Suy ra MNCD là hình bình hành.

MÀ MD = DC nên MNCD là hình thoi.

b) Xét tam giác EBC vuông tại E có EN là đường trung tuyến

Suy ra EN = BN = NC

Do đó tam giác ENC cân tại N

Mà NF là đường cao nên NF cũng là đường trung trực của tam giác ENC

Suy ra ME = MC hay tam giác EMC cân tại M.

c) Ta có:

 (hai góc so le trong)

(Tam giác EMC cân tại M)

(hai góc so le trong)

Suy ra

Lại có: MNCD là hình thoi nên  (CM là tia phân giác của )

ABCD là hình bình hành nên 

Vậy (đpcm).

---> Câu hỏi cùng bài:

• Bài 8 (sgk trang 89): Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC
• Bài 9 (sgk trang 89): Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm
• Bài 10 (sgk trang 89): Cho tam giác ABC vuông tại A (AB < AC)
• Bài 11 (sgk trang 89): Cho hình bình hành ABCD có AB = 2AD

---> Bài tiếp theo: Toán 8 Chân trời sáng tạo Chương 4 Bài 1: Thu thập và phân loại dữ liệu

----------------------------------------

Trên đây là lời giải chi tiết Bài 12 trang 89 Toán 8 Tập 1 CTST nằm trong bài Toán 8 Chân trời sáng tạo Bài tập cuối chương 3 cho các em học sinh tham khảo, nắm được cách giải các dạng bài tập của Chương 3: Định lí Pythagore. Các loại tứ giác thường gặp. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 8. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Đề thi giữa học kì 1 Toán 8, Đề thi học kì 1 Toán 8,.... Chúc các em học tốt.