Giaitoan.com Toán 8 Toán 8 Cánh diều

Bài 10 Trang 121 Toán 8 Tập 1 sách Cánh diều Bài tập cuối chương 5

Nội dung
  • 1 Đánh giá

Bài 10 Trang 121 Toán 8 Tập 1 CD

Bài 10 Trang 121 Toán 8 Tập 1 CD là lời giải chi tiết trong bài Bài tập cuối chương 5 SGK Toán 8 Cánh diều tạo giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Giải Bài 10 Trang 121 Toán 8 Tập 1

Bài 10 (sgk trang 121): Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.

Hướng dẫn:

Vận dụng định lí về tính chất và dấu hiệu nhận biết hình vuông.

Lời giải chi tiết:

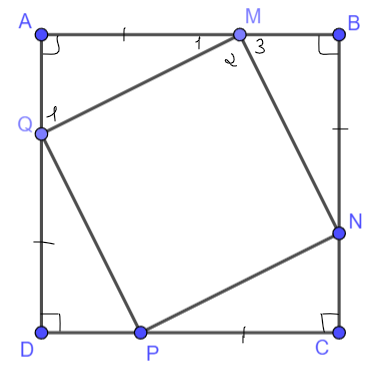
Ta có: AB = BC = CD = DA (ABCD là hình vuông)

AM = BN = CP = DG

Suy ra MB = NC = PD = QA

Xét tam giác AQM và tam giác BMN có:

AM = BN

\widehat{A} = \widehat{B}=90^{\circ}

AQ = BM

Do đó, ∆ AQM = ∆ BMN (cgc)

Suy ra QM = MN (hai cạnh tương ứng)

Chứng minh tương tự, suy ra QM = MN = NP = PQ

Ta có \widehat{Q_1} = \widehat{M_3} (∆ AQM = ∆ BMN)

Mặt khác: \widehat{Q_1} + \widehat{M_1} =90^{\circ} hay \widehat{M_1} + \widehat{M_3} =90^{\circ}

Do đó \widehat{M_2} =90^{\circ}

Xét tứ giác MNPQ có QM = MN = NP = PQ và \widehat{M_2} =90^{\circ}

Suy ra MNPQ là hình vuông (dhnb).

---> Câu hỏi cùng bài:

----------------------------------------

Trên đây là lời giải chi tiết Bài 10 Trang 121 Toán 8 CD Tập 1 nằm trong bài Bài tập cuối chương 5 cho các em học sinh tham khảo, nắm được cách giải các dạng bài tập của Chương 5: Định lí Pythagore. Tứ giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 8. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Đề thi giữa học kì 1 Toán 8, Đề thi học kì 1 Toán 8,.... Chúc các em học tốt.

Chia sẻ bởi: Hoa Đào
Mời bạn đánh giá!
  • Lượt xem: 29
Tìm thêm: Toán 8 Toán 8 Cánh diều
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần