Từ điểm M nằm ngoài (O;R), kẻ 2 tiếp tuyến MA, MB với đường tròn ( A v
à B là 2 tiếp điểm ) a. Chứng minh tứ giác MAOB nội tiếp b. Vẽ tia Mx nằm giữa 2 tia MA và MO. Tia Mx cắt (O;R) tại điểm C và điểm D ( điểm C nằm giữa 2 điểm M và D) . Chứng minh 2 tam giác MAC và tm giác MDA đồng dạng, rồi từ đó suy ra: MC/ MD = (AC/ AD)^2 c. Gọi H là giao điểm của OM và AB. Kẻ DK vuông góc với AB tại K, OP vuông góc với CD tại P, OQ vuông góc với HD tại Q. Chứng minh tứ giác HKPQ là hình thang cân

Hỏi bài
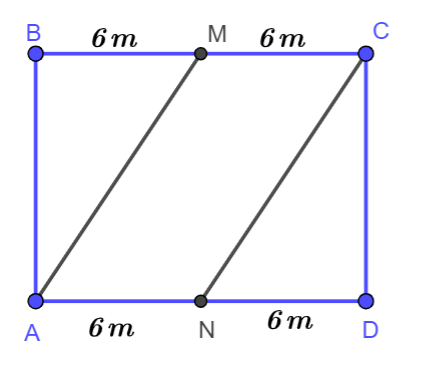
Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m, người ta phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở trong khu vực hình bình hành AMCN, cỏ sẽ trồng ở phần đất còn lại. Tiền công để trả cho mỗi mét vuông trồng hoa là 50 000 đồng, trồng cỏ là 40 000 đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
Ngày hỏi: 2 ngày trước 4 câu trả lời