Giaitoan.com Toán 8 Luyện tập Toán 8

Trường hợp đồng dạng thứ ba của tam giác Luyện tập Toán 8

Nội dung
  • 1 Đánh giá

Chuyên đề Toán 8: Tam giác đồng dạng

Bài tập Toán 9: Trường hợp đồng dạng thứ ba của tam giác ( g- g) là một dạng toán hình xuất hiện nhiều trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

1. Trường hợp đồng dạng thứ ba của tam giác

-Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng

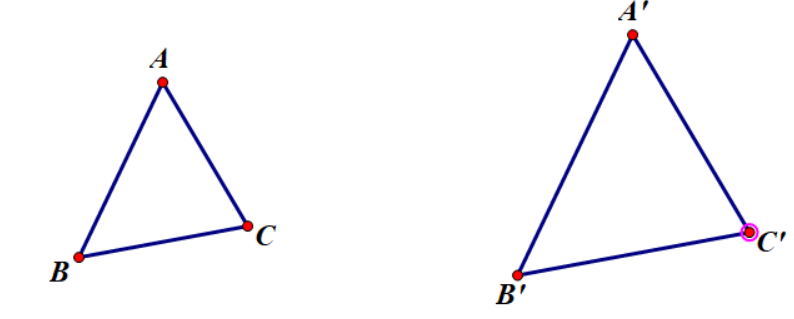
- Xét tam giác ABC và A’B’C có:

\left\{ \begin{array}{l} \widehat A = \widehat {{A^\prime }}\\ \widehat B = \widehat {{B^\prime }} \end{array} \right.  \Rightarrow \Delta ABC đồng dạng  \Delta {A^\prime }{B^\prime }{C^\prime }

2. Cách chứng minh tam giác đồng dạng

Ví dụ 1: Cho tam giác ABC, D là điểm trên cạnh AC sao cho \widehat {BDC} = \widehat {ABC}  ; AD = 7cm, DC = 9cm. Tính tỉ số \dfrac{{BD}}{{BA}}

Hướng dẫn giải

Xét \Delta CAB   và \Delta CBD có:

\widehat C là góc chung

\widehat {BDC} = \widehat {ABC} (gt)

\Rightarrow \Delta CAB  đồng dạng \Delta CBD \Rightarrow \dfrac{{CA}}{{CB}} = \dfrac{{AB}}{{BD}} = \dfrac{{CB}}{{CD}} \Rightarrow C{B^2} = CD.CA

Theo giả thiết ta có: CD = 9cm, AD = 7cm nên CA = CD + DA = 9 + 7 = 16 cm

Do đó C{B^2} = 9.16 = 144 \Rightarrow CB = 12\left( {cm} \right)

Mà \dfrac{{AB}}{{BD}} = \dfrac{{CB}}{{CD}} = \dfrac{{12}}{9} = \dfrac{4}{3} \Rightarrow \dfrac{{DB}}{{BA}} = \dfrac{3}{4}

Ví dụ 2: Cho hình vuông ABCD, gọi E, F theo thứ tự là trung điểm của AB, BC, CE cắt DF ở M. Tính tỉ số \dfrac{{{S_{\Delta CMD}}}}{{{S_{ABCD}}}}

Hướng dẫn giải

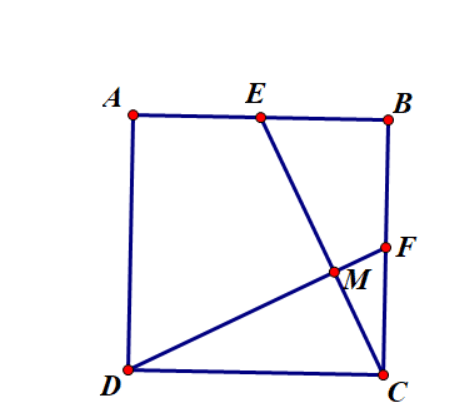
Xét \Delta DCF và  \Delta CBE có

DC = BC (gt) ( ABCD là hình vuông)

\widehat C = \widehat B = {90^ \circ } ( ABCD là hình vuông)

BE = CF ( E, F là trung điểm của AB và BC)

\Delta DCF = \Delta CBE\left( {c.g.c} \right) \Rightarrow \widehat {CDF} = \widehat {BCE}( 2 góc tương ứng)

Mà \widehat {DCE} + \widehat {ECB} = {90^ \circ } \Rightarrow \widehat {CDF} + \widehat {ECB} = {90^ \circ } \Rightarrow \Delta CMD vuông tại M

Xét  \Delta CMD và \Delta FCDcó

\widehat {CDF} = \widehat {BCE}

\widehat {CMD} = \widehat {FCD} = {90^ \circ }

\Rightarrow \Delta CMDđồng dạng \Delta FCD \Rightarrow \dfrac{{CD}}{{FD}} = \;\dfrac{{CM}}{{FC}}

Lại có\dfrac{{{S_{\Delta CMD}}}}{{{S_{\Delta FCD}}}} = \dfrac{{C{D^2}}}{{F{D^2}}} \Rightarrow {S_{\Delta CMD}} = \dfrac{{C{D^2}}}{{F{D^2}}}.{S_{\Delta FCD}}

Mà {S_{\Delta FCD}} = \dfrac{1}{2}CF.CD = \dfrac{1}{2}.\frac{1}{2}.BC.CD = .\dfrac{1}{4}C{D^2}

Vậy {S_{\Delta CMD}} = \dfrac{{C{D^2}}}{{F{D^2}}}.\dfrac{1}{4}C{D^2} = \dfrac{1}{4}\dfrac{{C{D^4}}}{{F{D^2}}}\,\,\,\left( * \right)

Áp dụng định lý Pi – ta – go trong tam giác vuông DFC, ta có:

D{F^2} = D{C^2} + C{F^2} = C{D^2} + {\left( {\dfrac{1}{2}BC} \right)^2} = \dfrac{5}{4}C{D^2}

Thay D{F^2} = \dfrac{5}{4}C{D^2} ta có:  {S_{\Delta CMD}} = \dfrac{1}{5}C{D^2} = \dfrac{1}{5}{S_{ABCD}}\, \Rightarrow \dfrac{{{S_{\Delta CMD}}}}{{{S_{ABCD}}}} = \dfrac{1}{5}

Ví dụ 3: Cho tam giác ABC có \widehat A = 2\widehat B. Đặt AB = c; AC = b, BC = a. Chứng minh rằng {a^2} = {b^2} + bc

Hướng dẫn giải

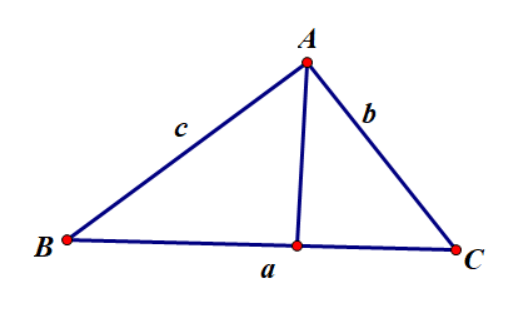
Kẻ AD là phân giác của góc A

Theo tính chất đường phân giác \dfrac{{CD}}{{DB}} = \dfrac{{AC}}{{AB}} \Rightarrow \dfrac{{CD}}{{DB + CD}} = \dfrac{{AC}}{{AB + AC}} \Rightarrow CD = \dfrac{{AC.BC}}{{AB + AC}} (1)

Xét \Delta ABC và \Delta DAC có:

\widehat {DAC} = \widehat B

\widehat Clà góc chung

\Delta ABC đồng dạng \Delta DAC \Rightarrow A{C^2} = BC.CD\,\,\,\left( 2 \right)

Thay (1) và (2) ta được A{C^2} = CB.\dfrac{{AC.BC}}{{AB + AC}}(đpcm)

Ví dụ 4: Cho tam giác ABC nhọn có đường cao CK. Dựng ra phía ngoài tam giác ABC hai tam giác ACE và CBF tương ứng vuông góc tại E, F và thỏa mãn  \widehat {ACE} = \widehat {CBA};\widehat {\,\,BCF} = \widehat {CAB}. Chứng minh C{K^2} = AE.BF

Hướng dẫn giải

Xét \Delta ACKvà \Delta CBF có:

\begin{array}{l} \widehat {CKA} = \widehat {BFC} = {90^ \circ }\\ \widehat {CAK} = \widehat {BCF} \end{array}

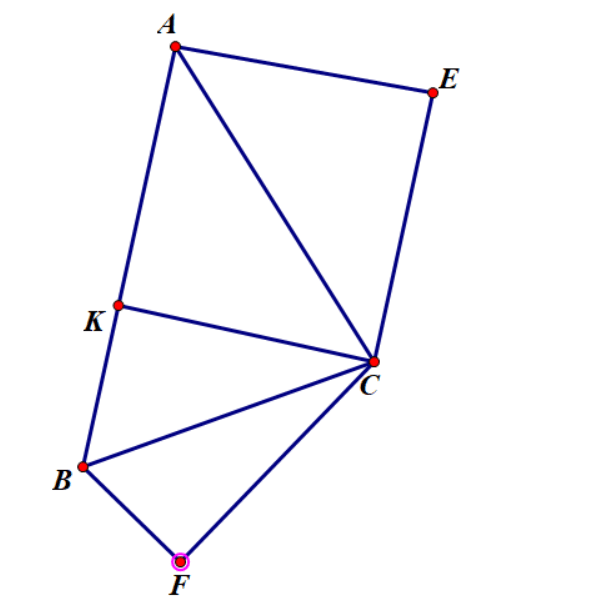
\Delta ACK đồng dạng \Delta CBF  (g – g )\Rightarrow \frac{{CK}}{{CA}} = \dfrac{{BF}}{{CB}}\,\,\,\left( 1 \right)

Tương tự ta chứng minh được:\Delta BCK đồng dạng với \Delta CAE \Rightarrow \dfrac{{CK}}{{CB}} = \dfrac{{AE}}{{AC}}\,\,\,\left( 2 \right)

Nhận từng vế của (1) và (2) ta được: \Rightarrow \dfrac{{CK}}{{CA}}.\dfrac{{CK}}{{CB}} = \dfrac{{BF}}{{BC}}\dfrac{{AE}}{{AC}}\,\,\, \Rightarrow C{K^2} = AE.BF

Ví dụ 5: Cho hình bình hành ABCD (AC > BD) vẽ CE vuông góc với AB tại E, CF vuông góc với AD tại F. Chứng minh rằng: AB. AE + AD. AF = A{C^2}

Hướng dẫn giải

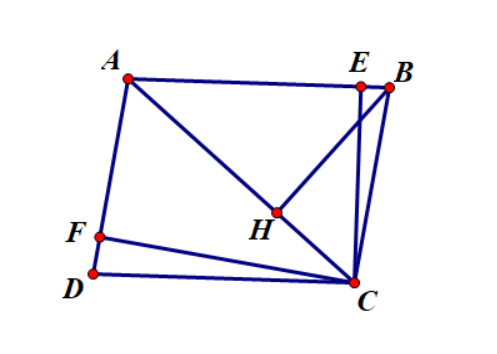
Vẽ BH \bot AC\left( {H \in AC} \right)

Xét \Delta ABH và \Delta ACE có:

\widehat {ABH} = \widehat {ACE} = {90^ \circ }

\widehat {BAC}là góc chung

\Delta ABH đồng dạng \Delta ACE \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AH}}{{AE}} \Rightarrow AB.AE = AC.AH\,\,\,\left( 1 \right)

Xét\Delta CHB  và \Delta CAFcó

\widehat {BCH} = \widehat {CAF}(so le trong)

\widehat {BHC} = \widehat {AFC} = {90^ \circ }

\Delta CHB đồng dạng \Delta CAF\Rightarrow \dfrac{{BC}}{{AC}} = \dfrac{{CH}}{{AF}} \Rightarrow BC.AF = AC.CH\,\,\,\left( 2 \right)

Cộng theo vế (1) và (2) ta được:

\begin{array}{l} AB.AE + BC.AF = AC.AH\, + AC.CH\,\,\\ \Rightarrow AB.AE + BC.AF = AC.\left( {AH\, + CH} \right) = AC.AC = A{C^2} \end{array}

Hy vọng tài liệu Tam giác đồng dạng lớp 8 sẽ giúp ích cho các bạn học sinh học nắm chắc kiến thức chuyên đề Đường tròn đồng thời học tốt môn Toán lớp 8. Chúc các bạn học tốt, mời các bạn tham khảo!

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 20
Tìm thêm: Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần