Tổng ba góc của một tam giác Bài tập Toán 7

1 Đánh giá

Tổng ba góc của một tam giác Toán 7

A. Tổng 3 góc của một tam giác
B. Bài tập Tổng ba góc của một tam giác

Trong chương trình Toán 7, học sinh sẽ thường xuyên gặp dạng bài Tính số đo góc B trong tam giác ABC khi biết độ lớn của góc A, góc C hay cho tam giác ABC vuông tại A biết góc B bằng 60⁰ tính các góc còn lại của tam giác, .... để giải các bài toán như trên, GiaiToan.com xin giới thiệu đến thầy cô và học sinh tài liệu Tổng 3 góc của 1 tam giác. Mời thầy cô và học sinh cùng tham khảo.

A. Tổng 3 góc của một tam giác

- Định lí: Tổng ba góc của một tam giác bằng 180⁰

- Định lí: Trong tam giác vuông, hai góc nhọn phụ nhau.

Ví dụ: Cho tam giác ABC vuông tại A.

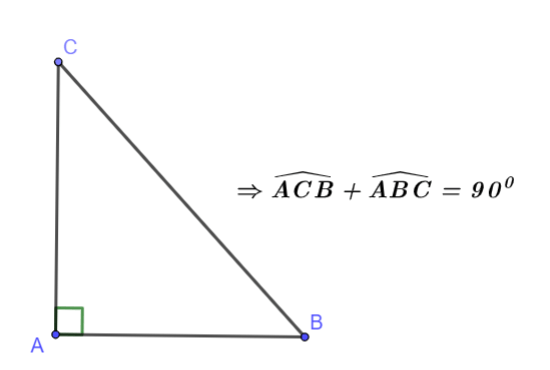
Tổng ba góc của một tam giác

- Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác ấy.

- Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

Chứng minh

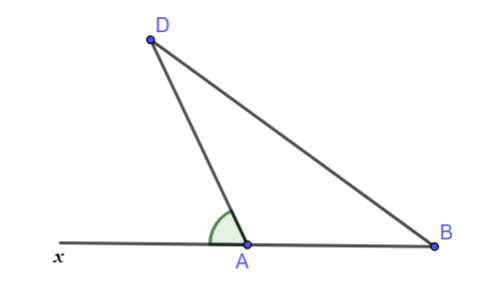
Tổng ba góc của một tam giác

Xét tam giác ADB có:

$\widehat {ADB} + \widehat {DBA} + \widehat {DAB} = {180^0} \Rightarrow \widehat {ADB} + \widehat {DBA} = {180^0} - \widehat {DAB}$

Mặt khác $\widehat {xAD} + \widehat {DAB} = {180^0} \Rightarrow \widehat {xAD} = {180^0} - \widehat {DAB}$ (Vì là hai góc kề bù)

$\Rightarrow \widehat {ADB} + \widehat {DBA} = \widehat {xAD}$

B. Bài tập Tổng ba góc của một tam giác

I. Bài tập trắc nghiệm

Câu 1: Cho tam giác ABC có . Số đo là bao nhiêu?

$A. \widehat{C}={{125}^{0}}$	$B. \widehat{C}={{115}^{0}}$
$C. \widehat{C}={{25}^{0}}$	$D. \widehat{C}={{95}^{0}}$

Câu 2: Cho tam giác ABC có ba góc bằng nhau. Hỏi mỗi góc có số đo bằng bao nhiêu?

$A. {{30}^{0}}$	$B. {{45}^{0}}$
$C. {{60}^{0}}$	$D. {{75}^{0}}$

Câu 3: Cho tia phân giác ABC, kẻ phân giác BM, CN cắt nhau tại K. Biết góc A có số đo là . Hỏi số đo góc bằng bao nhiêu?

$A. {{75}^{0}}$	$B. {{130}^{0}}$
$C. {{105}^{0}}$	$D. {{87}^{0}}$

Câu 4: Cho tam giác ABC, góc là góc ngoài đỉnh C. Khẳng định nào sau đây đúng?

$A. \widehat{A}+\widehat{B}<{{125}^{0}}$	$C. \widehat{A}+\widehat{B}>{{125}^{0}}$
$B. \widehat{A}+\widehat{B}={{125}^{0}}$	$D. \widehat{A}+\widehat{B}\ne {{125}^{0}}$

II. Bài tập tự luận

Câu 1: Cho tam giác ABC có , từ B vẻ BD vuông góc với AC, từ C kẻ CE vuông góc với AB, BD cắt CE tại K. Tính số đo góc , biết

Câu 2: Cho tam giác ABC biết góc . Kẻ tia phân giác BD và CE của hai góc B và C. Biết rằng . Tính số đo các góc của tam giác ABC.

Câu 3: Cho tam giác ABC có . Vẽ tia Am song song với BC, tia An là tia đối của tia AB và tia Am nằm giữa hai tia An, AC

a. Tính số đo góc

B. Tính số đo góc

c. Chứng minh Am là tia phân giác của góc

III. Lời giải bài tập Tổng ba góc của một tam giác

Đáp án bài tập trắc nghiệm

1. B

2.C

3.C

4.B

Đáp án bài tập tự luận

Câu 1:

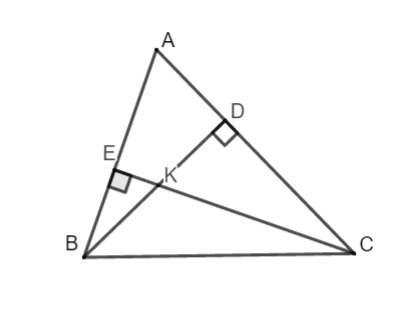Xét tam giác BCD vuông tại D ta có:

$\begin{align} & \widehat{DBC}+\widehat{DCB}={{90}^{0}}\Rightarrow \widehat{DBC}={{90}^{0}}-\widehat{DCB} \\ & \Rightarrow \widehat{DBC}=90-60={{30}^{0}} \\ \end{align}$

Tương tự xét tam giác BEC vuông tại E có:

$\begin{align} & \widehat{EBC}+\widehat{ECB}={{90}^{0}}\Rightarrow \widehat{ECB}={{90}^{0}}-\widehat{EBC} \\ & \Rightarrow \widehat{EBC}=90-70={{20}^{0}} \\ \end{align}$

Xét tam giác KCB có:

Tổng ba góc của một tam giác bằng ${{180}^{0}}$ nên ta có:

$\begin{align} & \widehat{KBC}+\widehat{KCB}+\widehat{BKC}={{180}^{0}}\Rightarrow \widehat{BKC}={{180}^{0}}-\left( {{20}^{0}}+{{30}^{0}} \right) \\ & \Rightarrow \widehat{BKC}={{130}^{0}} \\ \end{align}$

Do $\widehat{BKC}=\widehat{EKD}$ (đối đỉnh)

$\Rightarrow \widehat{EKD}={{130}^{0}}$

Câu 2:

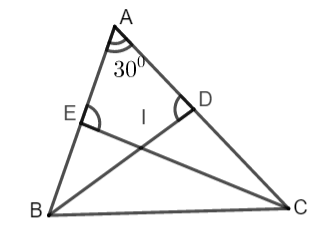Xét tam giác ADB có:

(1)

(theo định lí tổng ba góc của tam giác)

Xét tam giác AEC có:

(2)

(theo định lí tổng ba góc của tam giác)

Do (3)

Từ (1), (2), (3) ta có (4)

Do BD và CE là phân giác góc B và C nên

(5)

Từ (4) và (5) ta có:

Xét tam giác ABC có

$\begin{align} & \widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}} \\ & \Rightarrow \widehat{B}+\widehat{C}={{180}^{0}}-\widehat{A}={{180}^{0}}-{{30}^{0}}={{150}^{0}} \\ & \Rightarrow \widehat{B}=\widehat{C}=\frac{{{150}^{0}}}{2}={{75}^{0}} \\ \end{align}$

Câu 3:

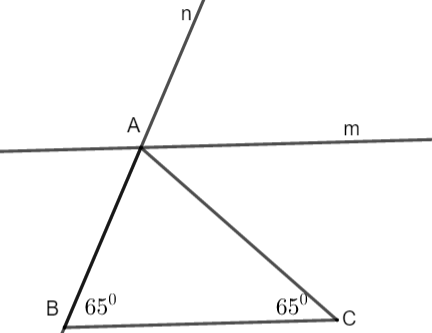a. Xét tam giác ABC có:

$\begin{align} & \widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}} \\ & \Rightarrow \widehat{A}={{180}^{0}}-\left( \widehat{B}+\widehat{C} \right)={{180}^{0}}-\left( {{65}^{0}}+{{65}^{0}} \right)={{50}^{0}} \\ \end{align}$

b. Ta có: Am song song với BC nên $\widehat{BCA}=\widehat{CAm}={{65}^{0}}$ (so le trong)

Mặt khác:

c. Ta có Am song song với BC nên (đồng vị) (1)

Theo câu b: (2)

Từ (1) và (2) suy ra

Vậy Am là tia phân giác của góc

------------------------------------------------------------

Hy vọng tài liệu Chuyên đề Toán 7: Tam giác sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết về các đường trong tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 7. Chúc các em học tốt.

Chia sẻ bởi: