Cách chứng minh 3 điểm thẳng hàng Chứng minh 3 điểm thẳng hàng
Cách chứng minh ba điểm thẳng hàng
GiaiToan.com biên soạn và đăng tải tài liệu Bài tập chứng minh ba điểm thẳng hàng lớp 7 giúp học sinh hiểu rõ thế nào là ba điểm thẳng hàng? Các cách chứng minh ba điểm thẳng hàng tiêu chuẩn nhất. Chi tiết mời các em học sinh cùng tham khảo. Chúc các bạn học tập tốt!
1. Ba điểm thẳng hàng
Ba điểm thẳng hàng là ba điểm cùng thuộc một đườn thẳng.
2. Các cách chứng minh 3 điểm thẳng hàng
Để chứng minh ba điểm thẳng hàng, chúng ta có thể sử dụng một số phương pháp sau đây
Phương pháp 1:
Nếu ![]() thì ba điểm A, B, C thẳng hàng
thì ba điểm A, B, C thẳng hàng
Phương pháp 2: Cơ sở Tiên đề Ơ-clit
Nếu AB // a, AC // a thì ba điểm A, B, C thẳng hàng
Phương pháp 3: Nếu hai tia OA, OB là tia phân giác của góc xOy thì ba điểm O, A, B thẳng hàng.
Phương pháp 4: Nếu AB ⊥ a, AC ⊥ a thì ba điểm A, B, C thẳng hàng
Phương pháp 5: Mỗi đoạn thẳng chỉ có 1 trung điểm
Nếu M là trung điểm của AB, M’ là giao điểm của AB và CD. Nếu M’ là trung điểm của AB
=> M trùng với M’
=> Ba điểm M, C, D thẳng hàng
3. Chứng minh ba điểm thẳng hàng
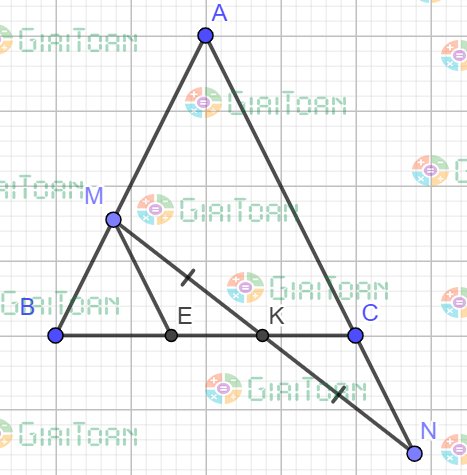
Ví dụ 1: Cho tam giác ABC cân tại A, Trên cạnh AB lấy điểm M. Trên tia đối của tia CA lấy điểm N sao cho MB = CN. Gọi K là trung điểm của MN, Chứng minh ba điểm B, K, C thẳng hàng.
Hướng dẫn giải
Cách 1: Kẻ ME // AC (điểm D thuộc BC)
=> ![]() (Hai góc đồng vị)
(Hai góc đồng vị)
Mà ![]()
Vậy tam giác MBE cân tại M
=> MB = ME
Kết hợp với giả thiết MB = NC ta suy ra ME = CN
Gọi K’ là giao điểm của BC và MN
Xét tam giác MEK’ và tam giác NCK’ có
![]() (so le trong của ME // AC)
(so le trong của ME // AC)
ME = CN (chứng minh trên)
![]()
=> ![]()
=> NK’ = MK’
Vậy K’ là trung điểm của MN => K trùng với K’
=> Ba điểm B, K, C thẳng hàng
Cách 2: Kẻ ME ⊥ BC, NF ⊥ BC
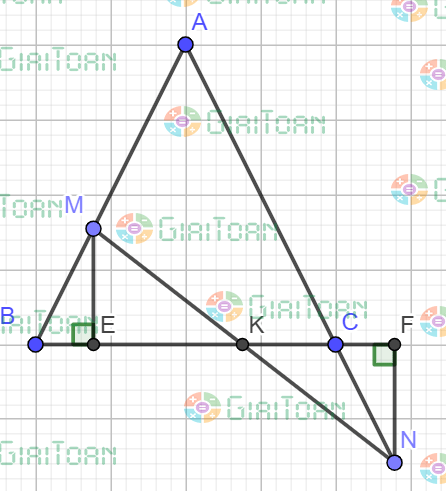
Xét tam giác BME và tam giác CNF vuông góc tại E và F ta có:
MB = CN
![]()
Vậy ![]()
=> ME = MF
Gọi K’ là giao điểm của BC và BN
Xét tam giác MEK’ và tam giác NFK’ vuông góc tại E và F ta có:
ME = NF
![]() (so le trong)
(so le trong)
=> ![]() => MK’ = NK’
=> MK’ = NK’
=> K’ là trung điểm của MN
=> K trùng với K’
=> Ba điểm B, K, C thẳng hàng.
Ví dụ 2: Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A. Vẽ các điểm D và E sao cho BD vuông góc và bằng BA, vuông góc và bằng BC. Gọi M là trung điểm của CE. Chứng minh ba điểm A, D, M thẳng hàng.
Hướng dẫn giải
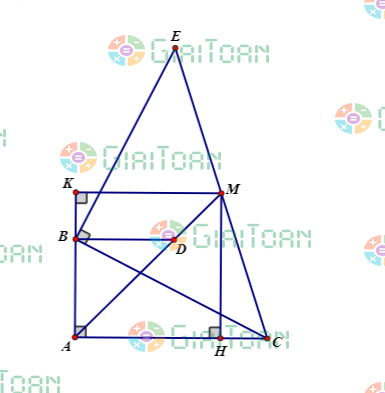
Kẻ MK ⊥ AB, MH ⊥ AC
Ta có M là trung điểm của CE
=> ![]()
Mặt khác ![]()
Mà ![]()
Ta lại có BM = MC => ![]() => MK = MH
=> MK = MH
=> ![]() (cạnh huyền – cạnh góc vuông)
(cạnh huyền – cạnh góc vuông)
=> ![]()
=> AM là tia phân giác của góc A
Mặt khác tam giác BAD vuông cân tại A
=> ![]()
=> AD là tia phân giác của góc A
=> A, D, M thẳng hàng (vì cùng thuộc tia phân giác góc A)
4. Bài tập chứng minh ba điểm thẳng hàng
Bài 1: Cho tam giác ABC có AB < AC kẻ tia phân giác AD của góc BAC. Trên cạnh AC lấy điểm E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a) ![]()
b) Chứng minh ba điểm E, F, D thẳng hàng
c) Chứng minh AD vuông góc với CF
Bài 2: Cho tam giác ABC vuông cân tại A. Vẽ ra phía ngoài tam giác ABC tam giác BCM cân tại M có góc ở đáy bằng 150. Trên nửa mặt phẳng AB chứa điểm C, vẽ tam giác đều ABN. Chứng minh ba điểm M, N, B thẳng hàng.
---------------------------------------------
Hy vọng tài liệu Cách chứng minh ba điểm thẳng hàng Toán 7 sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết, bài tập Làm quen với số liệu thống kê. từ đó vận dụng giải các bài toán Toán lớp 7 một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 7. Chúc các em học tốt.
- Lượt xem: 2.937






































