Giaitoan.com Toán 9 Lý thuyết Toán 9

Tính chất của hai tiếp tuyến cắt nhau Tiếp tuyến

Nội dung
  • 1 Đánh giá

Hai tiếp tuyến cắt nhau

Tiếp tuyến của đường tròn Toán 9 được xem là dạng toán căn bản quan trọng trong chương trình Toán 9 và đề thi tuyển sinh vào lớp 10. Tài liệu dưới đây do đội ngũ GiaiToan.com biên soạn và chia sẻ giúp học sinh hiểu rõ hơn về các dạng toán đường tròn lớp 9. Qua đó giúp các bạn học sinh ôn tập và rèn luyện cho kì thi tuyển sinh vào lớp 10 sắp tới. Mời các bạn học sinh và quý thầy cô cùng tham khảo!

1. Tiếp tuyến là gì?

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn

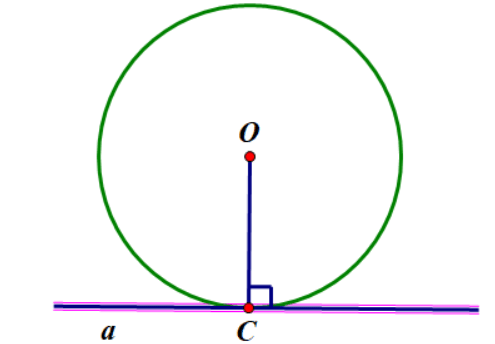
2. Tính chất của hai tiếp tuyến cắt nhau

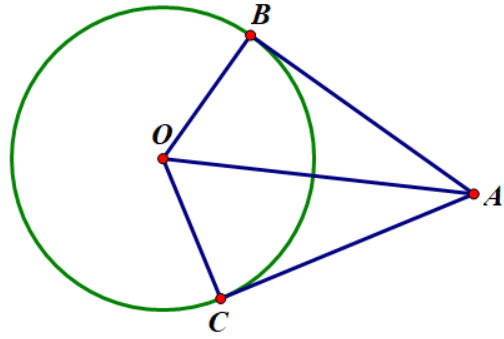
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai tiếp điểm

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm

Ví dụ 1: Cho đường tròn tâm O, bán kính R. Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với đường tròn O với B, C là tiếp điểm.

a) Chứng minh AO là đường trung trực của BC

b) Kẻ đường kính CD của (O). Chứng minh BD song song với AO

c) Kẻ OM vuông góc với OB ( M thuộc AC). Chứng minh MO = MA

Hướng dẫn giải

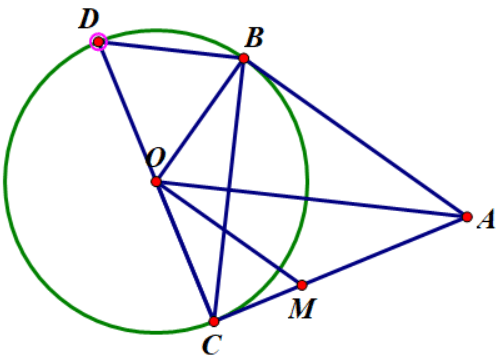
a) Ta có AB = AC ( tính chất hai tiếp tuyến cắt nhau) \Rightarrow tam giác ABC cân tại A

Mà \widehat {CAO} = \widehat {BAO} ( tính chất hai tiếp tuyến cắt nhau)

A thuộc đường trung trực của BC

Ta có OB = OC ( tính chất hai tiếp tuyến cắt nhau) \Rightarrow tam giác OBC cân tại O

Mà \widehat {COA} = \widehat {BOA} ( tính chất hai tiếp tuyến cắt nhau)

O thuộc đường trung trực của BC

AO là đường trung trực của BC

b) Ta có OB = OC = OD = \dfrac{1}{2}BC \Rightarrow tam giác BDC vuông tại B\Rightarrow DB \bot BC

Mà OA \bot BC ( cmt) \Rightarrow OA//BD

c) Ta có \widehat {COA} = \widehat {BOA}

Mà \widehat {BOA} = \widehat {MOA}\,\,\,\left( {OM//BA} \right) \Rightarrow \widehat {COA} = \widehat {MOA} \Rightarrow \DeltaMOA cân tại A

\RightarrowMO = MA

Hy vọng tài liệu tiếp tuyến sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi biểu thức chứa căn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo! Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Lý thuyết Toán 9, Luyện tập Toán 9, Giải toán 9, ...

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 75
Tìm thêm: Toán 9 Chuyên đề Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần