Giaitoan.com Toán 12 Toán 12 Chân trời sáng tạo

Thực hành 3 trang 18 Toán 12 tập 1 Chân trời sáng tạo Giải Toán 12 Chân trời sáng tạo Bài 2

Nội dung
  • 1 Đánh giá

Thực hành 3 trang 18 SGK Toán 12

Toán 12 Thực hành 3 trang 18 tập 1 trong bài Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số SGK Toán 12 Chân trời sáng tạo được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Thực hành 3 Toán 12 trang 18

Thực hành 3 trang 18 toán 12 tập 1: Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?

Lời giải chi tiết:

Giả sử độ dài một cạnh góc vuông là x (cm) (0 < x < 5)

=> Độ dài cạnh góc vuông còn lại là \sqrt{25-x^2} (cm)

Hàm số biểu thị diện tích tam giác là: S\left(x\right)=\frac{ 1}{ 2} x\sqrt{25-x^2}

Ta có: S'\left(x\right)=\frac{1}{2}\left(\sqrt{25-x^2}-\frac{x^2}{\sqrt{25-x^2}}\right)

S'(x) = 0 ⇔ x=\frac{5}{\sqrt{2}} (vì 0 < x < 5)

Lập bảng biến thiên của hàm số S(x):

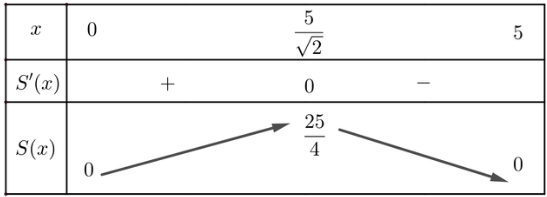
Vậy S(x) lớn nhất khi x=\frac{5}{\sqrt{2}}.

---> Câu hỏi cùng bài:

---------------------------------------

-------> Bài tiếp theo: Giải Toán 12 Chân trời sáng tạo Bài 3: Đường tiệm cận của đồ thị hàm số

Chia sẻ bởi: Captain
Mời bạn đánh giá!
  • Lượt xem: 108
Tìm thêm: Toán 12 Toán 12 Chân trời sáng tạo
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần