Bài toán: Giả thiết tạm kép Toán nâng cao - Toán tư duy 5

6 Đánh giá

Bài toán: Giả thiết tạm kép

1. Bài toán giả thiết tạm kép
2. Bài toán minh họa
3. Bài tập giả thiết tạm kép

Mục tiêu bài học

Giúp học sinh nhận diện được dạng toán giả thiết tạm kép
Áp dụng tốt lý thuyết vào các bài tập tự luyện

1. Bài toán giả thiết tạm kép

Khác với Giả thiết tạm đơn - bài toán chỉ có 2 đại lượng, bài toán giả thiết tạm kép đưa ra đến 3 đại lượng cho học sinh xử lý. Tuy nhiên các đại lượng trong đó có sự liên hệ với nhau bằng các tỉ lệ để học sinh dễ dàng đưa về bài toán hai đại lượng cơ bản. Chính vì vậy, giả thiết tạm kép thường có trong bài tập của các bạn học sinh lớp 5.

2. Bài toán minh họa

Bài toán: Có 18 xe ô tô gồm 3 loại: Loại 4 bánh chở được 5 tấn, loại 6 bánh chở được 8 tấn và loại 6 bánh chở được 10 tấn. 18 xe đó chở được tất cả 129 tấn hàng và có tổng 94 bánh. Hỏi có bao nhiêu xe mỗi loại?

Hướng dẫn:

Học sinh sẽ thấy bài toán có 3 đại lượng cần đi tìm:

+ Xe 4 bánh chở được 5 tấn

+ Xe 6 bánh chở được 8 tấn

+ Xe 6 bánh chở được 10 tấn.

Trong ba đại lượng này, ta thấy có 2 đại lượng xe 6 bánh giống nhau về số bánh, khác nhau về số tấn hàng chở được nên ta sẽ dùng phương pháp giả thiết tạm đơn đã học để xử lý 2 đại lượng này.

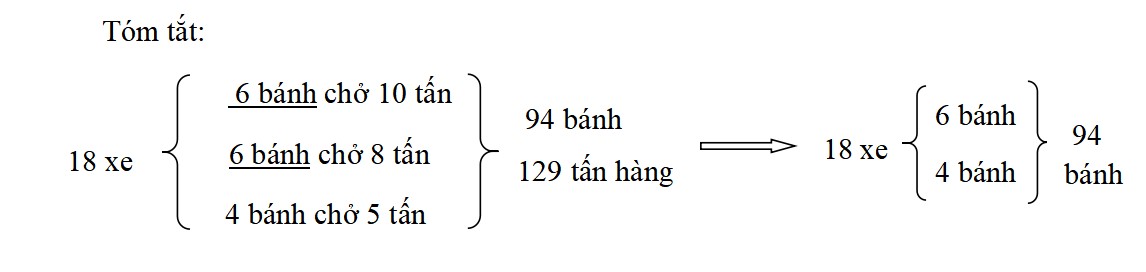
Vậy ở bài toán này chúng ta phải sử dụng đến 2 lần giả thiết tạm đơn.

+ Lần đầu, chúng ta dựa vào số bánh xe để tìm ra số xe 4 bánh

+ Lần tiếp, dựa vào số tấn hàng để tìm ra số lượng mỗi loại xe 6 bánh

Lời giải chi tiết:

Bài giải

Giả sử có tất cả 18 xe 6 bánh.

Khi đó tổng số bánh xe là:

18 x 6 = 108 (bánh xe)

Số bánh xe thừa ra là:

108 - 94 = 14 (bánh xe)

Khi ta thay một xe 6 bánh thành một xe 4 bánh thì tổng số bánh xe sẽ giảm đi:

6 - 4 = 2 (bánh xe)

Số xe 4 bánh là:

14 : 2 = 7 (xe)

Tổng số xe 6 bánh là:

18 - 7 = 11 (xe)

Số tấn hàng xe 4 bánh đã chở là:

7 x 5 = 35 (tấn)

Số tấn hàng mà xe 6 bánh chở được là:

129 - 35 = 94 (tấn)

Bài toán bây giờ trở thành:

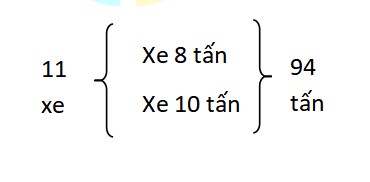
Giả sử có tất cả 11 xe loại 10 tấn.

Khi đó, 11 xe chở được số tấn hàng là:

10 x 11 = 110 (tấn hàng)

Số tấn hàng bị thừa ra là:

110 - 94 = 16 (tấn hàng)

Khi ta thay 1 xe chở 10 tấn hàng thành 1 xe chở 8 tấn hàng thì tổng số tấn hàng sẽ giảm đi:

10 - 8 = 2 (tấn)

Số xe chở được 8 tấn hàng là:

16 : 2 = 8 (xe)

Số xe chở được 10 tấn hàng là:

11 - 8 = 3 (xe)

Đáp số: 7 xe loại 4 bánh chở 5 tấn

8 xe loại 6 bánh chở 8 tấn

3 xe loại 6 bánh chở 10 tấn

3. Bài tập giả thiết tạm kép

Bài 1: Có 20 xe gồm 3 loại: xe máy 2 bánh có 2 chỗ ngồi, xe ô tô 4 bánh có 25 chỗ ngồi và xe ô tô 4 bánh có 18 chỗ ngồi. Người ta đếm được có 338 người trên xe và có tất cả 72 bánh xe. Biết rằng tất cả các xe đều được ngồi kín chỗ, hỏi mỗi loại có bao nhiêu xe?

Hướng dẫn:

Học sinh sẽ thấy bài toán có 3 đại lượng cần đi tìm:

+ Xe máy 2 bánh có 2 chỗ ngồi.

+ Xe ô tô 4 bánh có 25 chỗ ngồi.

+ Xe ô tô 4 bánh có 18 chỗ ngồi.

Mô tả bài toán bằng sơ đồ như sau:

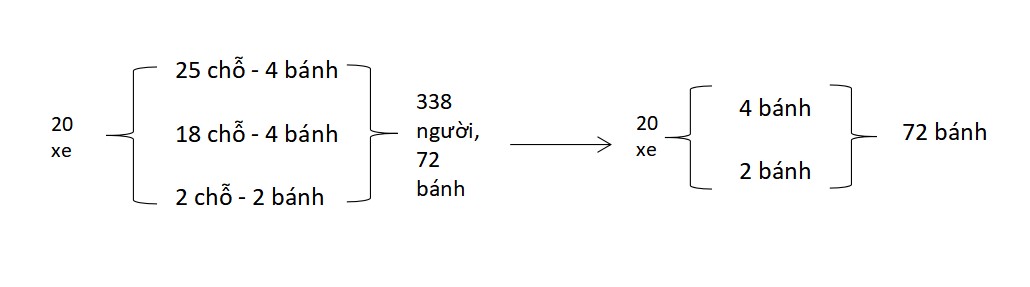
Vậy ở bài toán này chúng ta phải sử dụng đến 2 lần giả thiết tạm đơn.

+ Lần đầu, chúng ta dựa vào số bánh xe để tìm ra số xe máy 2 bánh

+ Lần tiếp, dựa vào số chỗ ngồi để tìm ra số lượng mỗi loại xe ô tô 4 bánh.

Lời giải chi tiết:

Bài giải

Giả sử, có tất cả 20 xe ô tô.

Khi đó, 20 xe có tất cả số bánh là:

20 x 4 = 80 (bánh xe)

Số bánh xe thừa ra là:

80 - 72 = 8 (bánh xe)

Khi ta thay 1 xe ô tô thành 1 xe máy, tổng số bánh xe sẽ giảm đi:

4 - 2 = 2 (bánh)

Có số xe máy là:

8 : 2 = 4 (xe)

Có số xe ô tô là:

20 - 4 = 16 (xe)

4 xe máy chở được số người là:

4 x 2 = 8 (chỗ ngồi)

16 xe ô tô chở được số người là:

338 - 8 = 330 (người)

Ta lại có tóm tắt như sau:

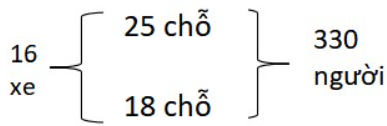
Giả sử tất cả 16 xe đều là loại 25 chỗ (chở 25 người)

Khi đó, 16 xe chở tất cả số người là:

25 x 16 = 400 (người)

Số người thừa ra là:

400 - 330 = 70 (người)

Khi ta thay 1 xe chở được 25 chỗ thành xe chở được 18 chỗ thì tổng số người sẽ giảm đi:

25 - 18 = 7 (người)

Tổng số xe loại 18 chỗ ngồi là:

70 : 7 = 10 (xe)

Tổng số xe loại 25 chỗ ngồi là:

16 - 10 = 6 (xe)

Đáp số: 4 xe máy;

10 xe ô tô loại 18 chỗ ngồi;

6 xe ô tô loại 25 chỗ ngồi.

Bài 2: Lớp em mua 50 vé xem phim gồm 3 loại: Loại 30 000 đồng, loại 50 000 đồng và loại

60 000 đồng hết tất cả 2 170 000 đồng. Biết số vé loại 30 000 đồng gấp 2 lần số vé loại 60 000 đồng.

Hướng dẫn:

Nhận xét: Ta thấy 1 vé loại 60 000 đồng thì sẽ phải có 2 vé loại 30 000 đồng

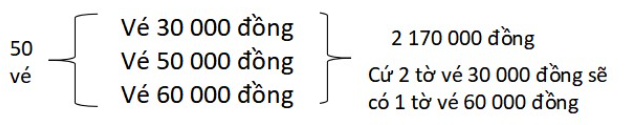
Với bài toán này ta chỉ cần sử dụng 1 lần giả thiết tạm đơn: tất cả số vé là loại 50 000 đồng

Khi đó, để số vé không thay đổi thì ta cần thay 3 vé 50 000 đồng thành 2 vé 30 000 và 1 vé 60 000 đồng (do số vé loại 30 000 đồng gấp đôi số vé loại 60 000 đồng).

Lời giải chi tiết:

Bài giải

Giả sử tất cả 50 vé đều là loại vé 50 000 đồng.

Khi đó, mua 50 vé sẽ hết số tiền là:

50 000 x 50 = 2 500 000 (đồng)

Số tiền thừa ra là:

2 500 000 - 2 170 000 = 330 000 (đồng)

(Do cứ 1 vé loại 60 000 đồng thì sẽ có 2 vé loại 30 000 đồng nên ta cần thay 3 vé 50 000 đồng thành 2 vé 30 000 và 1 vé 60 000 đồng)

Khi đó, tổng số tiền sẽ giảm đi:

50 000 x 3 - (30 000 x 2 + 60 000) = 30 000 (đồng)

Số vé loại 60 000 đồng là:

330 000 : 30 000 = 11 (vé)

Số vé loại 30 000 đồng là:

2 x 11 = 22 (vé)

Số vé loại 50 000 đồng là:

50 - (11 + 22) = 17 (vé)

Đáp số: 22 vé loại 30 000 đồng

17 vé loại 50 000 đồng

11 vé loại 60 000 đồng

Bài 3: Một bếp ăn nhập về 150 con vừa cua, ếch, và gà. Biết số con ếch gấp 2 lần số con gà. Ba loại có tất cả 860 chân. (Coi cua có 10 chân, ếch 4 chân và gà 2 chân).

Hướng dẫn:

Tương tự như Bài 2 ở trên: Ta thấy số con ếch gấp 2 lần số con gà nên ta cũng chỉ cần sử dụng 1 lần giả thiết tạm đơn: Bếp ăn nhập về 150 con cua.

Khi đó, để số lượng các con vật không thay đổi thì ta cần thay 3 con cua thành 2 con ếch và 1 con gà.

Lời giải chi tiết:

Bài giải

Giả sử bếp ăn đó nhập về 150 con cua.

Khi đó, 150 con sẽ có số chân là:

10 x 150 = 1 500 (chân)

Số chân thừa ra là:

1500 - 860 = 640 (chân)

Khi ta thay 3 con cua bằng 2 con ếch và 1 con gà thì tổng số chân sẽ giảm đi là:

10 x 3 - (4 x 2 + 2 x 1) = 20 (chân)

Số con gà là:

640 : 20 = 32 (con)

Số con ếch là:

32 x 2 = 64 (con)

Số con cua là:

150 - (32 + 64) = 54 (con)

Đáp số: 64 con ếch

54 con cua

32 con gà

Bài 4: Một cửa hàng đã bán được 211 kg kẹo gồm 3 loại: Loại kẹo 2kg, loại kẹo 3kg và loại kẹo 5kg. Biết có tổng 57 gói kẹo, số gói kẹo loại 3kg bằng trung bình cộng số gói kẹo loại 2kg và 5kg. Tính số gói kẹo mỗi loại?

Hướng dẫn:

Ta thấy số gói kẹo loại 3kg bằng trung bình cộng số gói kẹo loại 2kg và 5kg, tức là tổng số gói kẹo loại 2kg và 5kg gấp 2 lần loại 3kg. Ta có thể giải bài toán bằng bài toán tìm hai số khi biết tổng và tỉ số như sau:

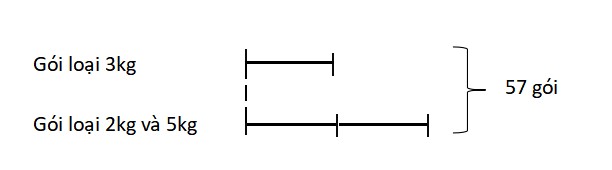
Sau khi tìm được số gói kẹo loại 2kg và 5kg, ta áp dụng bài toán Giả thiết tạm đơn để tìm số gọi kẹo loại 2kg và số gói kẹo loại 5kg.

Lời giải chi tiết:

Bài giải

Tổng số phần bằng nhau là:

2 + 1 = 3 (phần)

Số gói kẹo loại 3 kg là:

57 : 3 = 19 (gói)

Số gói kẹo loại 2kg và 5kg là:

19 x 2 = 38 (gói)

Khối lượng loại kẹo 3kg là:

19 x 3 = 57 (kg)

Khối lượng loại kẹo 2kg và 5kg là:

211 - 57 = 154 (kg)

Giả sử có tất cả 38 gói kẹo loại 5kg.

Khi đó, có tất cả số ki lô gam kẹo là:

5 x 38 = 190 (kg)

Số ki lô gam kẹo thừa ra là:

190 - 154 = 36 (kg)

Khi ta thay 1 gói kẹo 5kg bằng 1 gói kẹo 2kg thì tổng số ki lô gam kẹo giảm đi:

5 - 2 = 3 (kg)

Số gói kẹo loại 2kg là:

36 : 3 = 12 (gói)

Số gói kẹo loại 5kg là:

38 - 12 = 26 (gói)

Đáp số: 12 gói kẹo 2kg

19 gói kẹo 3kg

26 gói kẹo 5kg

--------------------------------------------------------

Như vậy, GiaiToan.com đã gửi tới các bạn học sinh phương pháp giải dạng toán Cấu tạo số tự nhiên một cách đầy đủ và chi tiết. Ngoài ra, các bạn học sinh có thể tham khảo thêm các tài liệu để luyện môn Toán 4 và luyện môn Toán 5 khác do GiaiToan biên soạn để học tốt môn Toán hơn.

Tham khảo thêm các tài liệu liên quan: