Giaitoan.com Toán 8 Luyện tập Toán 8

Diện tích xung quanh, diện tích toàn phần, thể tích hình lăng trụ đứng Công thức tính diện tích, thể tích của hình lăng trụ

Nội dung
  • 1 Đánh giá

Hình lăng trụ đứng

Diện tích xung quanh, diện tích toàn phần, thể tích hình lăng trụ đứng là tài liệu do GiaiToan. com biên soạn và gửi tới các bạn học sinh, giúp các bạn học sinh hiểu rõ hơn về hình lăng trụ đứng, và cách tính diện tích và thể tích của hình lăng trụ đứng để áp dụng tính toán trong các bài tập Toán 8, Toán 7. Mời các bạn học sinh cùng tham khảo bài viết.

1. Hình lăng trụ là gì?

- Hình lăng trụ là một đa diện gồm có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên song song hoặc bằng nhau

2. Hình lăng trụ đứng tứ giác

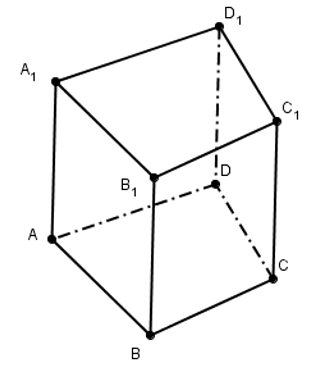                              Hình lăng trụ đứng ABCD \cdot {A_1}{B_1}{C_1}{D_1}

  • Các đỉnh: A,B,C,D,{A_1},{B_1},{C_1},{D_1}
  • Các mặt bên: AB{B_1}{A_1};BC{C_1}{B_1};CD{D_1}{C_1},A{A_1}D{D_1}
  • Các mặt đáy: ABCD;{A_1}{B_1}{C_1}{D_1}

2. Hình lăng trụ đứng tam giác

( Hình lăng trụ tam giác )

  • Các đỉnh: A, B, C, D, E, F
  • Các mặt bên ADCF, BCFE, ADEB,
  • Các mặt đáy ABC, DEF

3. Công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình lăng trụ

a) Diện tích xung quanh của hình lăng trụ

{S_{xq}} = 2ph

( với p là nửa chu vi đáy, h là chiều cao)

b) Diện tích toàn phần của hình lăng trụ

{S_{tp}} = {S_{xq}} + 2{S_{đáy}}

c) Thể tích của hình lăng trụ

V = S.h

( S là diện tích đáy, h là chiều cao)

Chú ý : Với mỗi đáy, ta sẽ có một công thức tính diện tích đáy và nửa chu vi đáy riêng biệt

4. Bài tập tính diện tích, thể tích của hình lăng trụ đứng

Ví dụ 1: Cho hình lăng trụ đứng ABCD \cdot {A_1}{B_1}{C_1}{D_1}  có đáy là ABCD là hình chữ nhật, biết chiều dài AB = 6cm, chiều rộng BC = 3 cm, chiều cao A{A_1} = 6cm . Tính

a) Diện tích xung quanh của hình lăng trụ đã cho

b) Thể tích hình lăng trụ đã cho

Hướng dẫn giải

a)

Chu vi của đáy ABCD là : ( 6 + 3 ) x 2 = 18 ( cm )

Nửa chu vi đáy là: 18 : 2 = 9 (cm)

Diện tích xung quanh của hình lăng trụ đó là: {S_{xq}} = 2ph = 2.9.6 = 108\left( {{m^2}} \right)

b)

Diện tích đáy ABCD là : 6.3 = 18\left( {{m^2}} \right)

Thể tich của hình lăng trụ đã cho là:  V = S.h = 6.18 = 108\left( {{m^3}} \right)

Ví dụ 2: Cho hình lăng trụ đứng tam giác ABC.{A^\prime }{B^\prime }{C^\prime } có đáy là tam giác cân tại A có các kích thước như hình vẽ. Tính thể tích của hình lăng trụ.

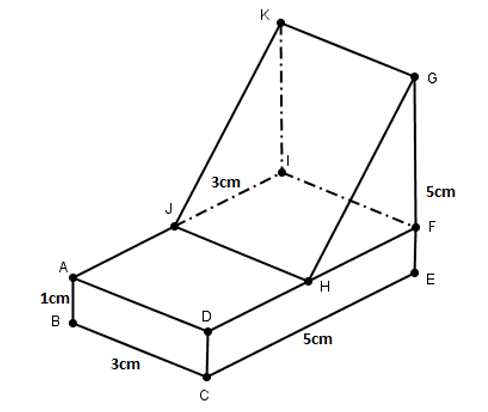
Hướng dẫn giải

Độ dài đường chéo của tam giác đáy là

JK = HG = \sqrt {{3^2} + {4^2}} = \sqrt {25} = 5{\rm{cm}}

Diện tích tam giác đáy:

{S_{\Delta HFG}} = {S_{\Delta TIK}} = \dfrac{1}{2}3.4 = 6{\rm{c}}{{\rm{m}}^2}

Diện tích toàn phần hình lăng trụ HFG.JIK

{S_{tp1}} = {S_{xq}} + 2{S_{đáy}} = 2\left( {\dfrac{{3 + 4 + 5}}{2}} \right) \cdot 3 + 2.6 = 48\,c{m^2}

* Tính diện tích toàn phần của hình hộp chữ nhật ABCD.EFI{I^\prime } (I’ là điểm phía dưới)

{S_{tp2}} = {S_{xq}} + 2{S_đáy} = 2(1 + 3).5 + 2.1.3 = 46\,c{m^2}

* {S_{JIFH}} = 3.3 = 9\,c{m^2}

* Diện tích toàn phần của hình đã cho là:

{S_{tp}} = {S_{tp1}} + {S_{tp2}} - {S_{MFH}} = 48 + 46 - 9 = 85\,c{m^2}

Thể tích hình lăng trụ:

{V_1} = {S_đáy} \cdot h = 6.3 = 18\,c{m^3}

Thể tích hình hộp chữ nhật:

{V_2} = {S_đáy} \cdot h = 3.5 = 15\,{\rm{c}}{{\rm{m}}^3}

Thể tích của hình đã cho là:

V = {V_1} + {V_2} = 18 + 15 = 33\,{\rm{c}}{{\rm{m}}^3}

-------------------------------------------

Như vậy, GiaiToan.com đã gửi tới các bạn học sinh Diện tích xung quanh, diện tích toàn phần, thể tích hình lăng trụ đứng. Ngoài ra, các bạn học sinh có thể tham khảo thêm các tài liệu và các công thức khác khác do GiaiToan biên soạn để học tốt môn Toán hơn tại Lý thuyết Toán 8, Giải toán 8, Luyện tập Toán 8,...........

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 110
Tìm thêm: Toán 8 Bài tập Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần