Đề kiểm tra học kì 2 môn Toán lớp 7 năm học 2020 - 2021 Đề số 3 Đề thi cuối kì 2 Toán 7

3 Đánh giá

Đề thi học kì 2 Toán 7

Đề thi cuối kì 2 Toán 7 năm học 2020 - 2021 - Đề 3
Đáp án đề thi cuối kì 2 Toán 7 năm học 2020 - 2021 - Đề 3

Đề thi toán lớp 7 học kì 2 năm học 2020 - 2021 - Đề 3 được biên soạn và đăng tải bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì Toán 7. Mời các bạn cùng tham khảo chi tiết. Chúc các em học sinh ôn tập thật tốt!

Đề thi cuối kì 2 Toán 7 năm học 2020 - 2021 - Đề 3

PHÒNG GD&ĐT ……..

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

Môn: Toán – Đề số 3

Thời gian: 90 phút

Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

I. Trắc nghiệm (2 điểm)

Câu 1: Cho đa thức A = 2x - 16 có nghiệm là:

A. x = 2

B. x = 8

C. x = -5

D. x = 4

Câu 2: Bậc của đa thức -2x² - 3x⁵ - 3x³ + x⁴ + 3x⁵ + x - 1

A. 5

B. 4

C. 3

D. 2

Câu 3: Ba độ dài nào dưới đây là độ dài ba cạnh của một tam giác:

A. 2cm, 6cm, 4cm	B. 2cm, 3cm, 4cm
C. 2cm, 3cm, 5cm	D. 1cm, 3cm, 5cm

Câu 4: Đơn thức nào dưới đây đồng dạng với đơn thức $\frac{1}{2}{x^2}{z^3}$

A. $4{x^2}{z^3}$	B. $- \frac{1}{2}{x^3}{z^2}$
C. $\frac{1}{2}x{z^2}$	D. $- \frac{1}{4}{x^3}{z^3}$

Câu 5: Cho tam giác ABC có thì quan hệ giữa các cạnh trong tam giác ABC là:

A. AC < BC < AB	B. AC > AB > BC
C. AC < AB < BC	D. AB < AC < BC

Câu 6: Cho tam giác ABC có AM là đường trung tuyến, G là trọng tâm tam giác. Đẳng thức nào sau đây sai?

A. AG/AM = 2/3	B. MG/AM = 1/3
C. AG/MG = 1/2	D. MG / AG = 1/2

II. Tự luận (8 điểm)

Câu 1: (1,5 điểm) Thời gian làm bài kiểm tra môn Toán của một lớp học được thống kê trong bảng số liệu dưới đây.

Thời gian (phút)	5	6	7	8	9	10	12
Tần số	2	4	9	5	x	8	7	N = ?

a. Dấu hiệu cần tìm hiểu ở đây là gì?

b. Tìm x, N? Biết thời gian trung bình là 8,2 phút

c. Mốt của dấu hiệu là bao nhiêu?

Câu 2: (1,5 điểm) Cho đơn thức: $A = \left( {8{y^3}{x^2}} \right).\left( { - \frac{1}{2}{x^3}yz} \right),B = \left( {2{x^2}y} \right)\left( {\frac{{ - 1}}{{14}}{x^3}{y^3}z} \right)$

a. Thu gọn đơn thức A, B

b. Chứng minh hai đơn thức trên đồng dạng.

Câu 3: (2 điểm) Cho các đa thức:

A(x) = 4x² - 3x⁴ + 8 + 2x⁴+ x³ - 2x²

B(x) = x⁴ + 2x³ - 2x² + 3x³ + x - 6

a. Thu gọn và sắp xếp các đa thức A(x) và B(x) theo lũy thừa giảm dần của biến.

b. Tìm hệ số bậc cao nhất, hệ số tự do, bậc của đa thức C(x) = A(x) – 2B(x).

Câu 4: (2,5 điểm) Cho tam giác ABC cân tại B $\left( {\widehat B < {{90}^0}} \right)$ . Kẻ AH vuông góc với BC , CK vuông góc với AB $\left( {H \in BC} \right)$ , M là giao điểm của AH và CK.

a. Chứng minh AH = CK

b. Chứng minh tam giác ACM cân.

c. Trên tia CK lấy điểm D sao cho DK = KC. Chứng minh $\widehat {ADC} = \widehat {CAH}$

Câu 5: Tìm giá trị nhỏ nhất của biểu thức:

T = |a - 2015| + |a - 2016| + |a - 2017|

Đáp án đề thi cuối kì 2 Toán 7 năm học 2020 - 2021 - Đề 3

I. Phần Trắc nghiệm

1.B

2.B

3.D

4.A

5.C

6.C

II. Phần Tự luận

Câu 1:

a. Dấu hiệu: Thời gian làm bài kiểm tra môn Toán của một lớp học.

b. x = 3, N = 38

c. Mốt của dấu hiệu: 10

Câu 2:

a. $A = - 4{x^5}{y^4}z$

$B = - \frac{1}{7}{x^5}{y^4}z$

b. HS tự chứng minh

Câu 3:

A(x) = - x⁴ + x³ + 2x² + 8

B(x) = x⁴ + 5x³ - 2x² + x - 6

b. C(x) = -3x⁴ - 9x³ + 6x²- 2x + 20

Câu 4:

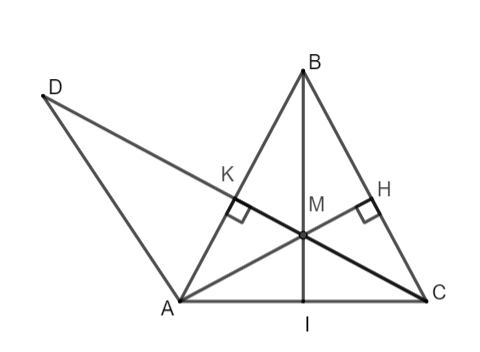
Đề thi Toán lớp 7 học kì 2 năm 2020 - 2021 Đề 3

a. Chứng minh hai tam giác ABH và tam giác BKC bằng nhau (ch - gn).

b. Suy ra từ câu a cặp cạnh AM = MC tương ứng bằng nhau.

c. Ta có tam giác ACD có AK vừa là đường trung tuyến vừa là đường cao nên tam giác ADC cân tại A, kết hợp với hai góc ở đáy của tam giác MAC bằng nhau

$\Rightarrow \widehat {ADC} = \widehat {CAH}$

Câu 5:

T = |a - 2015| + |a - 2016| + |a - 2017|

=> T = (|a - 2015| + |a - 2017|) + |a - 2016|

|a - 2015| + |a - 2017| ≥ |a - 2015 + 2017 - a| = 2

Dấu bằng xảy ra khi: 2015 ≤ a ≤ 2017 (*)

Ta lại có |a - 2016| ≥ 0 dấu bằng xảy ra khi x = 2016 (**)

Từ (*) và (**) ta có GTNN của T bằng 2

Dấu bằng xảy ra khi và chỉ khi x = 2016.

(Còn tiếp)

Mời các bạn tải tài liệu miễn phí tham khảo hướng dẫn giải chi tiết!

Mời bạn đọc tham khảo thêm tài liệu liên quan:

---------------------------------------------------------

Trên đây là Đề thi học kì 2 môn Toán 7 năm học 2020 - 2021 Đề 3 được giaitoan.com giới thiệu tới quý thầy cô và bạn đọc. Hi vọng tài liệu này giúp các em học sinh lớp 7 tự ôn luyện và vận dụng các kiến thức đã học vào việc giải bài tập toán. Chúc các em học tốt.