Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 3 Đề kiểm tra giữa kì 1 toán 8

1 Đánh giá

Đề thi giữa kì 1 Toán 8 có đáp án - Đề 3

Đề thi Toán giữa kì 1 lớp 8
Đáp án Đề thi Toán giữa kì 1 lớp 8

Đề thi giữa kì 1 Toán 8 năm học 2021 - 2022 Đề số 3 được Giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì môn Toán 8. Mời các bạn cùng tham khảo chi tiết!

Để tải đề thi, mời ấn vào đường link sau: Đề thi toán lớp 8 giữa kì 1 - Đề 3

A. Đề thi Toán giữa kì 1 lớp 8

Bản quyền thuộc về GiaiToan
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

Câu 1 (2 điểm) 1. Rút gọn biểu thức: ${\left( {2x + 1} \right)^2} - 2\left( {2x - 1} \right)\left( {2x + 1} \right) + {\left( {2x - 1} \right)^2}$

2. Thực hiện phép chia:

$\left( {{a^5} - 3{a^4} - {a^2} + 5{a^3} + 3a - 5} \right):\left( { - 3a + {a^2} + 5} \right)$

3. Chứng minh biểu thức sau không phụ thuộc vào biến:

$6\left( {3x - 4} \right) - 5\left( {x - 3} \right) - 19x + 3\left( {2x - 1} \right)$

Câu 2 (2 điểm) Phân tích đa thức thành nhân tử

a. ${x^2} - 6x - {y^2} + 9$	b. $2x - 8xy + 8x{y^2}$
c. ${x^4} + 2{x^2}y + {y^2} - 9$

Câu 3 (2 điểm) Tìm giá trị của x, biết:

a. ${\left( {x + 3} \right)^2} - 4x - 17 = \left( {x + 2} \right)\left( {x - 2} \right)$

b. $\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) - 1 = 0$

Câu 4 (1 điểm)

1. Tìm m để đa thức $2{x^3} - 3{x^2} + x + m$ chia hết cho đa thức x + 1.

2. Cho hai số không âm a và b thỏa mãn ${a^2} + {b^2} = a + b$ . Tính giá trị lớn nhất của biểu thức:

$A = \frac{a}{{a + 1}} + \frac{b}{{b + 1}}$

Câu 5 (3 điểm) Cho hình bình hành ABCD có AD = 2AB. Từ C kẻ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M kẻ MF vuông góc với CE, MF vuông góc với BC tại N.

a. Tứ giác MNCD là hình gì?

b. Tam giác CME là tam giác gì?

c. Chứng minh $\widehat {BAD} = 2\widehat {AEM}$

B. Đáp án Đề thi Toán giữa kì 1 lớp 8

Câu 1 (2 điểm)

1. ${\left( {2x + 1} \right)^2} - 2\left( {2x - 1} \right)\left( {2x + 1} \right) + {\left( {2x - 1} \right)^2}$

$\begin{matrix} = {\left[ {\left( {2x + 1} \right) - \left( {2x - 1} \right)} \right]^2} \hfill \\ = {\left[ {2x + 1 - 2x + 1} \right]^2} \hfill \\ = {2^2} = 4 \hfill \\ \end{matrix}$

$\begin{matrix} \left( {{a^5} - 3{a^4} + 5{a^3}} \right) + \left( { - {a^2} + 3a - 5} \right) \hfill \\ = {a^3}\left( {{a^2} - 3a + 5} \right) - \left( {{a^2} - 3a + 5} \right) \hfill \\ = \left( {{a^2} - 1} \right)\left( {{a^2} - 3a + 5} \right) \hfill \\ \Rightarrow \left( {{a^5} - 3{a^4} - {a^2} + 5{a^3} + 3a - 5} \right):\left( { - 3a + {a^2} + 5} \right) = {a^2} - 1 \hfill \\ \end{matrix}$

$\begin{matrix} 6\left( {3x - 4} \right) - 5\left( {x - 3} \right) - 19x + 3\left( {2x - 1} \right) \hfill \\ = 18x - 24 - 5x + 15 - 19x + 6x - 3 \hfill \\ = \left( {18x - 5x - 19x + 6x} \right) + \left( { - 24 + 15 - 3} \right) \hfill \\ = 0x - 12 = - 12 \Rightarrow dpcm \hfill \\ \end{matrix}$

Câu 2 (2 điểm)

a. ${x^2} - 6x - {y^2} + 9 = \left( {{x^2} - 6x + 9} \right) - {y^2} = {\left( {x - 3} \right)^2} - {y^2} = \left( {x - 3 - y} \right)\left( {x - 3 + y} \right)$

b. $2x - 8xy + 8x{y^2} = 2x\left( {1 - 4y + 4{y^2}} \right) = 2x{\left( {1 - 2y} \right)^2}$

$\begin{matrix} {x^4} + 2{x^2}y + {y^2} - 9 \hfill \\ = \left( {{x^4} + 2{x^2}y + {y^2}} \right) - {3^2} \hfill \\ = {\left( {{x^2} + y} \right)^2} - {3^2} \hfill \\ = \left( {{x^2} + y - 3} \right)\left( {{x^2} + y + 3} \right) \hfill \\ \end{matrix}$

Câu 3 (2 điểm)

a) ${\left( {x + 3} \right)^2} - 4x - 17 = \left( {x + 2} \right)\left( {x - 2} \right)$

$\begin{matrix} \Rightarrow {x^2} + 6x + 9 - 4x - 17 = {x^2} - 4 \hfill \\ \Rightarrow {x^2} + 6x + 9 - 4x - 17 - {x^2} + 4 = 0 \hfill \\ \Rightarrow 2x - 4 = 0 \hfill \\ \Rightarrow x = 2 \hfill \\ \end{matrix}$

Vậy x = 2

b) $\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 4} \right) - 1 = 0$

$\begin{matrix} \Rightarrow {x^3} - 27 - {x^3} + 4x - 1 = 0 \hfill \\ \Rightarrow 4x - 28 = 0 \hfill \\ \Rightarrow x = 7 \hfill \\ \end{matrix}$

Vậy x = 7

Câu 4:

1) $\left( {2{x^3} - 3{x^2} + x + m} \right):\left( {x + 1} \right) = 2{x^2} - 5x + 6$ dư (m – 6)

Để phép chia là phép chia hết thì m – 6 = 0

=> m = 6

2) $\left\{ {\begin{array}{*{20}{c}} {{a^2} + 1 \geqslant 2a} \\ {{b^2} + 1 \geqslant 2b} \end{array} \Rightarrow {a^2} + {b^2} + 2 \geqslant 2a + 2b \Rightarrow a + b \leqslant 2} \right.$

Chứng minh được với hai số dương m, n bất kì thì $\frac{1}{m} + \frac{1}{n} \geqslant \frac{4}{{m + n}}$

$A = \frac{a}{{a + 1}} + \frac{b}{{b + 1}} = 2 - \left( {\frac{1}{{a + 1}} + \frac{1}{{b + 1}}} \right) \leqslant 2 - \frac{4}{{a + 1 + b + a}} \leqslant 1$

Do đó:

Vậy GTLN của A là 1, đạt được khi a = b = 1

Câu 5:

Hình vẽ minh họa:

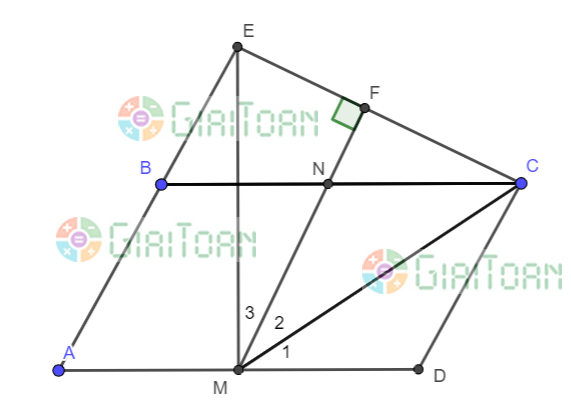
Đề thi giữa kì 1 Toán 8 năm học 2021 - 2022 Đề số 3

a) Ta có: $\left\{ {\begin{array}{*{20}{c}} {CE \bot AB} \\ {MF \bot EC} \end{array} \Rightarrow MF//AB//CD} \right.$ => MNCD là hình bình hành

Ta lại có: $MD = \frac{1}{2}AD = AB = CD$ => MNCD là hình thoi

b) Từ chứng minh trên ta có:

$CN = CD = \frac{1}{2}BC;NF//BE \Rightarrow EF = FC$

Tam giác CME có FM vừa là đường cao vừa là đường trung tuyến là tam giác CME là tam giác cân tại M.

c) Ta có:

$\left\{ {\begin{array}{*{20}{c}} {\widehat {BAD} = \widehat {NMD}\left( {dv} \right)} \\ {\widehat {NMD} = \widehat {{M_1}} + \widehat {{M_2}} = 2\widehat {{M_3}}} \\ {\widehat {{M_3}} = \widehat {AEM}\left( {slt} \right)} \end{array}} \right. \Rightarrow \widehat {BAD} = 2\widehat {AEM}$