Giaitoan.com Toán 8 Luyện tập Toán 8

Bất đẳng thức tam giác Luyện tập toán 8

Nội dung
  • 1 Đánh giá

Bất đẳng thức tam giác

Chuyên đề Toán 8: Bất đẳng thức tam giác và các ví dụ cụ thể, giúp các bạn học sinh lớp 8 ôn tập và củng cố kiến thức về dạng toán về bất đẳng thức. Tài liệu bao gồm công thức, các dạng toán, các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề đa thức Toán lớp 8. Chúc các bạn học tập hiệu quả!

1. Bất đẳng thức tam giác là gì?

Trong một tam giác bất kỳ, tổng độ dài hai cạnh bao giờ cũng lớn hơn độ dài cạnh còn lại

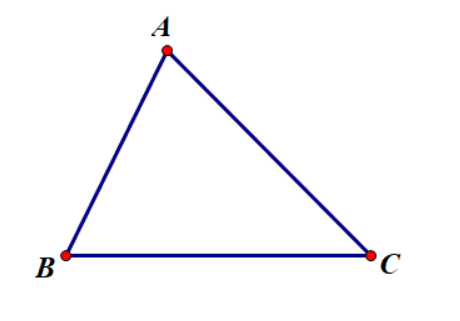
- Xét tam giác ABC ta có:

AB + AC > BC

AB + BC > AC

AC + BC > AB

2. Bài tập bất đẳng thức

Ví dụ 1: Cho a, b, c là độ dài ba cạnh của 1 tam giác. Chứng minh rằng\dfrac{a}{{b + c}} + \dfrac{b}{{a + c}} + \dfrac{c}{{a + b}} < 2

Hướng dẫn giải

Ta có \dfrac{a}{{b + c}} < 1 \Rightarrow \dfrac{a}{{b + c}} < \dfrac{{2a}}{{a + b + c}}

Tương tự ta có: \dfrac{b}{{c + a}} < 1 \Rightarrow \dfrac{b}{{c + a}} < \dfrac{{2b}}{{a + b + c}};\dfrac{c}{{a + b}} < 1 \Rightarrow \dfrac{c}{{a + b}} < \dfrac{{2c}}{{a + b + c}}

Cộng vế theo vế ta được

\dfrac{a}{{b + c}} + \dfrac{b}{{c + a}} + \dfrac{c}{{a + b}} < \dfrac{{2a}}{{a + b + c}} + \dfrac{{2b}}{{a + b + c}} + \dfrac{{2c}}{{a + b + c}} = \dfrac{{2\left( {a + b + c} \right)}}{{a + b + c}} = 2

Vậy \dfrac{a}{{b + c}} + \dfrac{b}{{a + c}} + \dfrac{c}{{a + b}} < 2

Ví dụ 2: Cho a, b, c > 0. Chứng minh rằng: 1 < \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2

Hướng dẫn giải

Ta có : \dfrac{a}{{a + b + c}} < \dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}

Tương tự ta có:

\dfrac{b}{{a + b + c}} < \dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}

\dfrac{c}{{a + b + c}} < \dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}

Cộng theo vế ta được:

\begin{array}{l} \dfrac{a}{{a + b + c}} + \dfrac{b}{{a + b + c}} + \dfrac{c}{{a + b + c}} < M < \dfrac{{a + b}}{{a + b + c}} + \dfrac{{b + c}}{{a + b + c}} + \dfrac{{c + a}}{{a + b + c}}\\ \Rightarrow \dfrac{{a + b + c}}{{a + b + c}} < M < \dfrac{{2\left( {a + b + c} \right)}}{{a + b + c}}\\ \Rightarrow 1 < M < 2 \end{array}

Ví dụ 3: Cho tam giác ABC có độ dài ba cạnh là a, b,c chu vi là 2p. Chứng minh rằng: \dfrac{{abc}}{8} \ge \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)

Hướng dẫn giải

Ta có \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \ge 2\sqrt {\left( {p - a} \right)\left( {p - b} \right)} \Rightarrow c \ge 2\sqrt {\left( {p - a} \right)\left( {p - b} \right)}

Chứng minh tương tự ta có: a \ge 2\sqrt {\left( {p - b} \right)\left( {p - c} \right)}

và b \ge 2\sqrt {\left( {p - a} \right)\left( {p - c} \right)}

Nhân theo vế ta được: abc \ge 8\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)

Ví dụ 4: Cho a + b + c = 1. Chứng minh rằng: {a^2} + {b^2} + {c^2} \ge \frac{1}{3}

Hướng dẫn giải

Đặt\left\{ \begin{array}{l} a = x + \dfrac{1}{3}\\ b = y + \dfrac{1}{3}\\ c = z + \dfrac{1}{3} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {a^2} = {x^2} + \dfrac{2}{3}x + \dfrac{1}{9}\\ {b^2} = {y^2} + \dfrac{2}{3}y + \dfrac{1}{9}\\ {c^2} = {z^2} + \dfrac{2}{3}z + \dfrac{1}{9} \end{array} \right. .

Cộng theo vế ta được {a^2} + {b^2} + {c^2} = {x^2} + {y^2} + {z^2} + \frac{2}{3}\left( {x + y + z} \right) + \dfrac{1}{3}\,\,\,\left( 1 \right)

Mà a + b + c = x + y + z + 1 \Rightarrow x + y + z = 0. Thay vào (1) ta được {a^2} + {b^2} + {c^2} = {x^2} + {y^2} + {z^2} + \dfrac{1}{3} \ge \dfrac{1}{3}\,

(đpcm)

Ví dụ 5: Cho a, b,c > 0 thỏa mãn \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \le a + b + c . Tìm GTLN của T = \dfrac{1}{{2 + {a^2}}} + \dfrac{1}{{2 + {b^2}}} + \dfrac{1}{{2 + {c^2}}}

Hướng dẫn giải

Ta có:

2T = \left( {1 - \dfrac{{{a^2}}}{{2 + {a^2}}}} \right) + \left( {1 - \dfrac{{{b^2}}}{{2 + {b^2}}}} \right) + \left( {1 - \dfrac{{{c^2}}}{{2 + {c^2}}}} \right) = 3 - \left( {\dfrac{{{a^2}}}{{2 + {a^2}}} + \dfrac{{{b^2}}}{{2 + {b^2}}} + \dfrac{{{c^2}}}{{2 + {c^2}}}} \right) = 3 - A

Áp dụng BĐT Cauchy – Schawzr ta có:

A \ge \dfrac{{a + b + c}}{{{a^2} + {b^2} + {c^2} + 6}} = \dfrac{{{a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)}}{{{a^2} + {b^2} + {c^2} + 6}}\,\,\left( 1 \right)

Mà abc\left( {a + b + c} \right) \ge ab + bc + ca \Rightarrow {\left( {ab + bc + ca} \right)^2} \ge 3abc\left( {a + b + c} \right) thay vào (1) ta được A \ge 1 \Rightarrow 2T \le 2 \Rightarrow T \le 1

-------------------------------------

Hi vọng Chuyên đề bất đẳng thức Toán 8 là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình lớp 8 cũng như ôn luyện cho các kì thi sắp tới. Mời thầy cô và bạn đọc tham khảo thêm một số tài liệu liên quan: Hỏi đáp Toán 8, Lý thuyết Toán 8, Giải Toán 8, Luyện tập Toán 8, ... Chúc các bạn học tốt!

Chia sẻ bởi: Lê Thị Thùy
Mời bạn đánh giá!
  • Lượt xem: 303
Tìm thêm: Bài tập Toán 8 Toán 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần