Bài Toán tìm quy luật dãy số cách đều và dãy hình Toán nâng cao lớp 4, 5

GiaiToan xin giới thiệu tới các em bài Toán nâng cao lớp 5 Tìm quy luật dãy số cách đều và dãy hình. Tài liệu này bao gồm đầy đủ các quy luật dãy số thường gặp có cách giải chi tiết và các dạng bài tập tự luyện cho các em học sinh tham khảo, rèn luyện kỹ năng giải Toán 5. Dưới đây là nội dung chi tiết, các em tham khảo nhé.

I. Lý thuyết cần nắm

1. Phân loại các dãy số cách đều thường gặp:

a. Dãy số tự nhiên

Ví dụ 1: 0; 1; 2; 3; 4;....

b. Dãy số chẵn, lẻ.

Ví dụ 2: 

• Dãy số chẵn: 0; 2; 4; 6; 8;....
• Dãy số lẻ: 1; 3; 5; 7; 9;....

c. Dãy số chia hết hoặc không chia hết cho một số tự nhiên nào đó.

Ví dụ 3:

• Dãy gồm các số chia hết cho 3: 0; 3; 6; 9; 12;...
• Dãy gồm các số chia 7 dư 1: 1; 8; 15; 22; 29;...

2. Một số dãy số không cách đều nhưng có quy luật:

a. Dãy có tổng (hiệu) giữa hai số liên tiếp là một dãy số.

Ví dụ 4: 1; 4; 9; 16; 25; 36;....

Đây là dãy có hiệu giữa hai số liên tiếp là một dãy số.

Thật vậy: ; ; ; ; ....

Hiệu của hai số liên tiếp tạo thành một dãy số phụ là: 3; 5; 7; 9; 11;... đây là một dãy số cách đều

b. Dãy nhóm

• Hàng ngang: (1); (2; 3); (4; 5; 6); (7; 8; 9)...
• Hàng dọc:            1

2     3

4      5      6

...

c.  Dãy phân số 

Tham khảo chi tiết tại đây:  Dãy phân số và cách tính nhanh dãy phân số 

d. Dãy hình

Trong một số bài toán, thay vì cho các số trực tiếp, đề bài cho dãy các hình và yêu cầu các em tìm ra quy luật của dãy

Ví dụ 5:

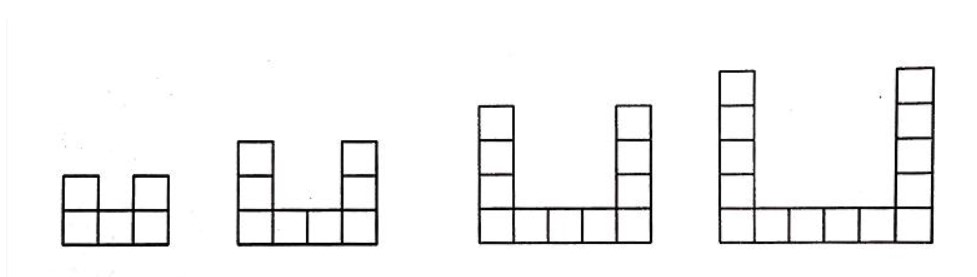
Đếm số hình vuông ta được dãy số sau: 5; 8; 11; 14

II. Bài tập

Bài 1a: Điền thêm 3 số hạng vào dãy số sau: 1, 3, 4, 7, 11, 18, 29, 47,...

Hướng dẫn:

Muốn giải được bài toán trên trước hết phải xác định quy luật của dãy số như sau: Ta thấy:

1 + 3 = 4; 3 + 4 = 7; 4 + 7 = 11; 7 + 11 = 18; 11 + 18 = 29

Dãy số trên được lập theo quy luật sau: Kể từ số hạng thứ ba trở đi mỗi số bằng tổng của hai số hạng đứng liền trước nó.

Ba số hạng tiếp theo là 29 + 47= 76; 47+ 76= 123; 76+ 123= 199

Vậy dãy số được viết đầy đủ là: 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199.

Bài 1b (học sinh tự luyện): Viết tiếp 3 số hạng vào dãy số sau: 1, 2, 3, 6, 11, 20

Bài 2a: Tìm các số còn thiếu trong dãy số sau: 3; 5; 9;...;...; 65

Hướng dẫn 

Ta thấy:

Quy luật của dãy số là: Kể từ số hạng thứ 2 trở đi, mỗi số hạng gấp 2 lần số liền trước nó trừ đi 1. Vậy tương tự ta sẽ có:

Vậy dãy số đầy đủ là: 3; 5; 9; 17; 33; 65

Bài 2b (học sinh tự luyện): Điền các số còn thiếu vào chỗ chấm: 4; 7; 13; 25;..;...; 193

Bài 3a: Viết 3 số tiếp theo của dãy số sau: 1; 4; 9; 16; 25;...;...;...;

Hướng dẫn 

Các em học sinh xem lại Ví dụ 4 để tìm ra quy luật. GiaiToan xin giới thiệu một quy luật khác như sau:

Ta thấy ; ; ; ; 

Dãy số trên được lập theo quy luật sau: Mỗi số hạng đều được viết lại thành tích của một số với chính nó

Vậy 3 số tiếp theo sẽ là:

Dãy số đầy đủ là: 1; 4; 9; 16; 25; 36; 49; 64

Bài 3b (học sinh tự luyện): Điền các số còn thiếu của dãy số sau: 2; 6; 12; 20;...;...;...; 72

Bài 4a: Cho dãy số sau: 1; 2; 4; 5; 7; 8; 10; 11; 13;....;....;....;.... Viết tiếp 4 số hạng của dãy số trên

Hướng dẫn

Ta thấy: Bắt đầu từ số đầu tiên, hai số cạnh nhau là hai số tự nhiên liên tiếp. Ta viết lại dãy số thành nhóm như sau:

(1; 2); (4; 5); (7; 8); (10; 11)

Tiếp theo, ta thấy các nhóm tạo thành hai dãy số phụ cách đều. Dãy 1 gồm các số 1; 4; 7; 10;...

Dãy 2 gồm các số 2; 5; 8; 11;...

Vậy nhóm tiếp theo là (13; 14); (16; 17)

Dãy số đầy đủ là: 1; 2; 4; 5; 7; 8; 10; 11; 13; 14; 16; 17

Bài 4b (học sinh tự luyện): Viết tiếp 3 số hạng vào dãy số sau: 2; 5; 8; 11; 14; 17;.....;......;......

Bài 5a: Hình tiếp theo có bao nhiêu tam giác màu xám?

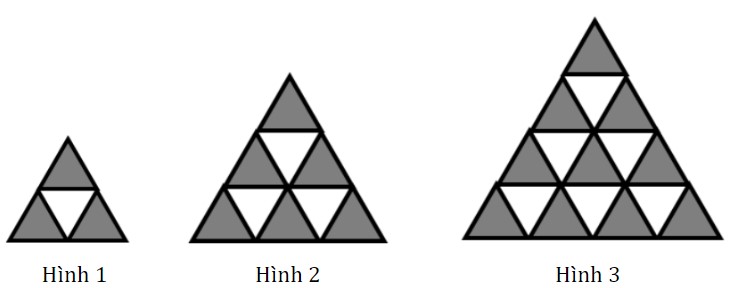
Hướng dẫn

Ta đếm số tam giác màu xám theo thứ tự được dãy số sau: 3; 6; 10

Ta thấy quy luật dãy số như sau: Hiệu hai số liên tiếp tạo thành một dãy số cách đều 3; 4; 5;...

Vậy hình tiếp theo sẽ có hình tam giác màu xám

Bài 5b (học sinh tự luyện): Hình tiếp theo có bao nhiêu ô vuông màu xanh?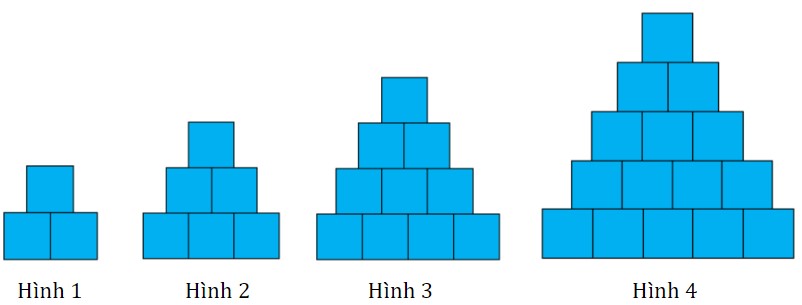

Tham khảo thêm các tài liệu liên quan đến dãy số cách đều:

• Bài toán tính tổng của dãy số có quy luật cách đều Toán lớp 5
• Tìm số hạng thứ n của dãy số cách đều

Như vậy, GiaiToan.com đã gửi tới các bạn học sinh cách tìm quy luật của dãy số cách đều và dãy hình. Ngoài ra, các bạn học sinh có thể tham khảo thêm các tài liệu để luyện môn Toán 5 khác do GiaiToan biên soạn để học tốt môn Toán hơn.