Giaitoan.com Toán 9 Chuyên đề Toán 9 thi vào 10

Bài tập tỉ số lượng giác của góc nhọn Chuyên đề Toán lớp 9 luyện thi vào lớp 10

Nội dung
  • 1 Đánh giá

Tỉ số lượng giác của góc nhọn

Chuyên đề Toán 9: Hệ thức lượng trong tam giác là một dạng toán khó thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được  GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

Công thức hệ thức lượng

A. Công thức tỉ số lượng giác của góc nhọn

Bài tập tỉ số lượng giác của góc nhọn

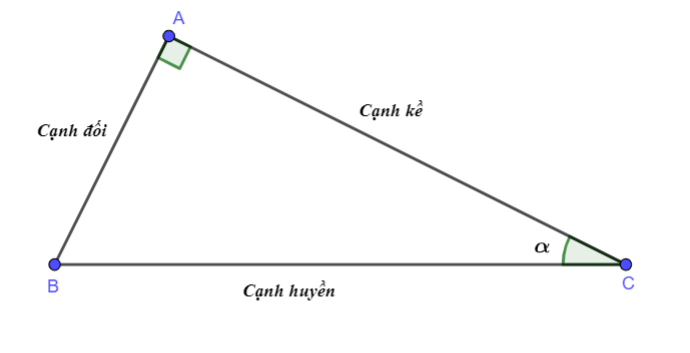
Các tỉ số lượng giác của góc nhọn được định nghĩa như sau:

\sin \alpha = \frac{{AB}}{{BC}};\cos \alpha = \frac{{AC}}{{BC}};\tan \alpha = \frac{{AB}}{{AC}};\cot \alpha = \frac{{AC}}{{AB}}

+ Nếu là một góc nhọn thì

0 < \sin \alpha < 1;0 < \cos \alpha < 1;

\tan \alpha > 0;\cot \alpha > 0

2. Với hai góc \alpha ,\beta mà \alpha + \beta = {90^0}

Ta có: \sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta

Nếu hai góc nhọn \alpha ,\beta có \sin \alpha = \sin \beta hoặc \cos \alpha = \cos \beta thì \alpha = \beta

3. {\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1

4. Với một số góc đặc biệt ta có:

\sin {30^0} = \cos {60^0} = \frac{1}{2};\sin {45^0} = \cos {45^0} = \frac{{\sqrt 2 }}{2}

\cos {30^0} = \sin {60^0} = \frac{{\sqrt 3 }}{2};\cot {60^0} = \tan {30^0} = \frac{1}{{\sqrt 3 }}

\tan {45^0} = \cot {45^0} = 1;\cot {30^0} = \tan {60^0} = \sqrt 3

B. Tính tỉ số lượng giác của góc nhọn

Ví dụ 1. Biết \sin \alpha = \frac{5}{{13}}. Tính \cos \alpha ,\tan \alpha và \cot \alpha.

Hướng dẫn giải

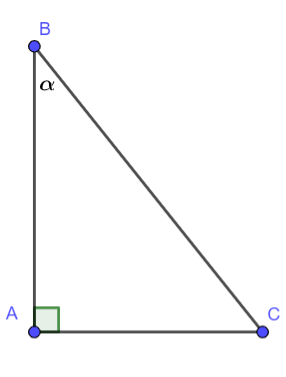
Bài tập tỉ số lượng giác của góc nhọn

Cách 1. Xét tam giác ABC vuông tại A.

Đặt \widehat B = \alpha. Ta có: \sin \alpha = \frac{{AC}}{{BC}} = \frac{5}{{13}}

=> \frac{{AC}}{5} = \frac{{BC}}{{13}} = k

=> AC = k, BC = 13k.

Tam giác ABC vuông tại A nên:

A{B^2} = B{C^2} - A{C^2} = {\left( {13k} \right)^2} - {\left( {5k} \right)^2} = 144{k^2}

=> AB = 12k

Vậy \cos \alpha = \frac{{AB}}{{BC}} = \frac{{12k}}{{13k}} = \frac{{12}}{{13}}; \tan \alpha = \frac{{AC}}{{AB}} = \frac{{5k}}{{12k}} = \frac{5}{{12}}; \cot \alpha = \frac{{AB}}{{AC}} = \frac{{12k}}{{5k}} = \frac{{12}}{5}

Cách 2. Ta có \sin \alpha = \frac{5}{{13}} => {\sin ^2}\alpha = \frac{{25}}{{169}}

Mà {\sin ^2}\alpha + {\cos ^2}\alpha = 1

=> {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - \frac{{25}}{{169}} = \frac{{144}}{{169}}

=> \cos \alpha = \frac{{12}}{{13}}

=> \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{5}{{13}}:\frac{{12}}{{13}} = \frac{5}{{13}}.\frac{{13}}{{12}} = \frac{5}{{12}}

=> \cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{12}}{{13}}:\frac{5}{{13}} = \frac{{12}}{{13}}.\frac{{13}}{5} = \frac{{12}}{5}

Ở cách giải thứ nhất ta biểu thị độ dài các cạnh của tam giác ABC theo đại lượng k rồi sử dụng định nghĩa tỉ số lượng giác của góc nhọn để tính \cos \alpha ,\tan \alpha ,\cot \alpha. Ở cách giải thứ hai, ta sử dụng giả thiết \sin \alpha = \frac{5}{{13}} để tính {\sin ^2}\alpha rồi tính \cos \alpha từ {\sin ^2}\alpha + {\cos ^2}\alpha = 1. Sau đó ta tính \tan \alpha và \cot \alpha qua \sin \alpha và \cos \alpha.

Ví dụ 2. Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tạiH. Biết HD : HA = 1 : 2. Chứng minh rằng tanB . tan C = 3

Hướng dẫn giải

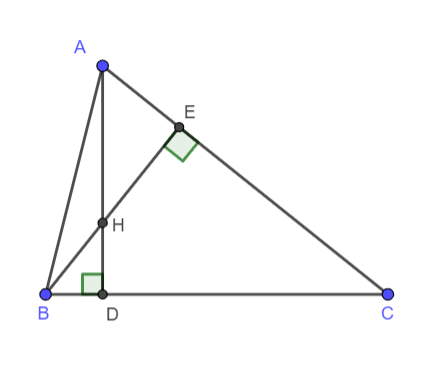
Bài tập tỉ số lượng giác của góc nhọn

Ta có: \tan B = \frac{{AD}}{{BD}};\tan C = \frac{{AD}}{{CD}}

=> \tan B.\tan C = \frac{{A{D^2}}}{{BD.CD}} (1)

\widehat {HBD} = \widehat {CAD} (cùng phụ với \widehat {ACB})

\widehat {HDB} = \widehat {ADC} = {90^0}

=> \Delta BDH \sim \Delta ADC (g.g)

=> \frac{{DH}}{{DC}} = \frac{{BD}}{{AD}}

=> BD . DC = DH . AD (2)

Từ (1) và (2)

=> \tan B.\tan C = \frac{{A{D^2}}}{{DH.AD}} = \frac{{AD}}{{DH}} (3).

Theo giả thiết \frac{{HD}}{{AH}} = \frac{1}{2} suy ra \frac{{HD}}{{AH + HD}} = \frac{1}{{2 + 1}} hay \frac{{HD}}{{AD}} = \frac{1}{3}

=> AD = 2HD. Thay vào (3) ta được: \tan B.\tan C = \frac{{3HD}}{{DH}} = 3

Ví dụ 3. Biết \sin \alpha .\cos \alpha = \frac{{12}}{{25}}. Tính \sin \alpha ,\cos \alpha

Hướng dẫn giải

Biết \sin \alpha .\cos \alpha = \frac{{12}}{{25}}. Để tính \sin \alpha ,\cos \alpha ta cần tính \sin \alpha + \cos \alpha rồi giải phương trình với ẩn là \sin \alpha hoặc \cos \alpha.

Ta có:

{\left( {\sin \alpha + \cos \alpha } \right)^2} = {\sin ^2}\alpha + {\cos ^2}\alpha + 2\sin \alpha .\cos \alpha = 1 + 2.\frac{{12}}{{25}} = \frac{{49}}{{25}}

=> \sin \alpha + \cos \alpha = \frac{7}{5} nên \sin \alpha = \frac{7}{5} - \cos \alpha

=> \cos \alpha \left( {\frac{7}{5} - \cos \alpha } \right) = \frac{{12}}{{25}} \Leftrightarrow \frac{7}{5}\cos \alpha - {\cos ^2}\alpha = \frac{{12}}{{25}}

\begin{matrix} \Leftrightarrow 25{\cos ^2}\alpha - 35\cos \alpha + 12 = 0 \hfill \\ \Leftrightarrow 5\cos \alpha \left( {5\cos \alpha - 4} \right) - 3\left( {5\cos \alpha - 4} \right) = 0 \hfill \\ \Leftrightarrow \left( {5\cos \alpha - 4} \right)\left( {5\cos \alpha - 3} \right) = 0 \hfill \\ \end{matrix}

=> \cos \alpha = \frac{4}{5} hoặc \cos \alpha = \frac{3}{5}

+ Nếu \cos \alpha = \frac{4}{5} thì \sin \alpha = \frac{{12}}{{25}}:\frac{4}{5} = \frac{3}{5}

+ Nếu \cos \alpha = \frac{3}{5} thì \sin \alpha = \frac{{12}}{{25}}:\frac{3}{5} = \frac{4}{5}

Vậy \sin \alpha = \frac{3}{5},  \cos \alpha = \frac{4}{5} hoặc \sin \alpha = \frac{4}{5},\cos \alpha = \frac{3}{5}

------------------------------------------

Hy vọng tài liệu Công thức tỉ số lượng giác lớp 9 sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi biểu thức chứa căn đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Chia sẻ bởi: Đường tăng
Mời bạn đánh giá!
  • Lượt xem: 542
Tìm thêm: Toán 9 Bài tập Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần