Bài 2.15 trang 32 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống Giải Toán 10 Kết nối tri thức

3 Đánh giá

Bài 2.15 trang 32 SGK Toán 10

Toán lớp 10 Bài 2.15 trang 32 là lời giải bài tập cuối chương 2 trang 31 SGK Toán 10 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 2.15 Toán 10 trang 32

Bài 2.15 (SGK trang 32): Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu: trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm. Vì lí do giảm thuế, bác An muốn số tiền đầu tư lãi suất chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu được sau một năm là lớn nhất?

Hướng dẫn giải

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết

Gọi số tiền bác An đầu tư cho trái phiếu chính phủ là x (triệu đồng)

S ố tiền bác An đầu tư cho trái phiếu ngân hàng là y (triệu đồng)

Điều kiện: 0 ≤ x ≤ 1 200, 0 ≤ y ≤ 1 200

Khi đó bác An đầu tư cho trái phiếu doanh nghiệp là 1 200 – x – y (triệu đồng)

Vì lí do giảm thuế, bác An muốn số tiền đầu tư lãi suất chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có: x ≥ 3y hay x – 3y ≥ 0.

Để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên ta có:

1 200 – x – y ≤ 200

=> x + y ≥ 1 000

Ta có hệ bất phương trình: $\left\{ {\begin{array}{*{20}{c}} {0 \leqslant x \leqslant 1200} \\ {0 \leqslant y \leqslant 1200} \\ {x - 3y \geqslant 0} \\ {x + y \geqslant 1000} \end{array}} \right.$

Hình vẽ biểu diễn miền nghiệm của hệ bất phương trình:

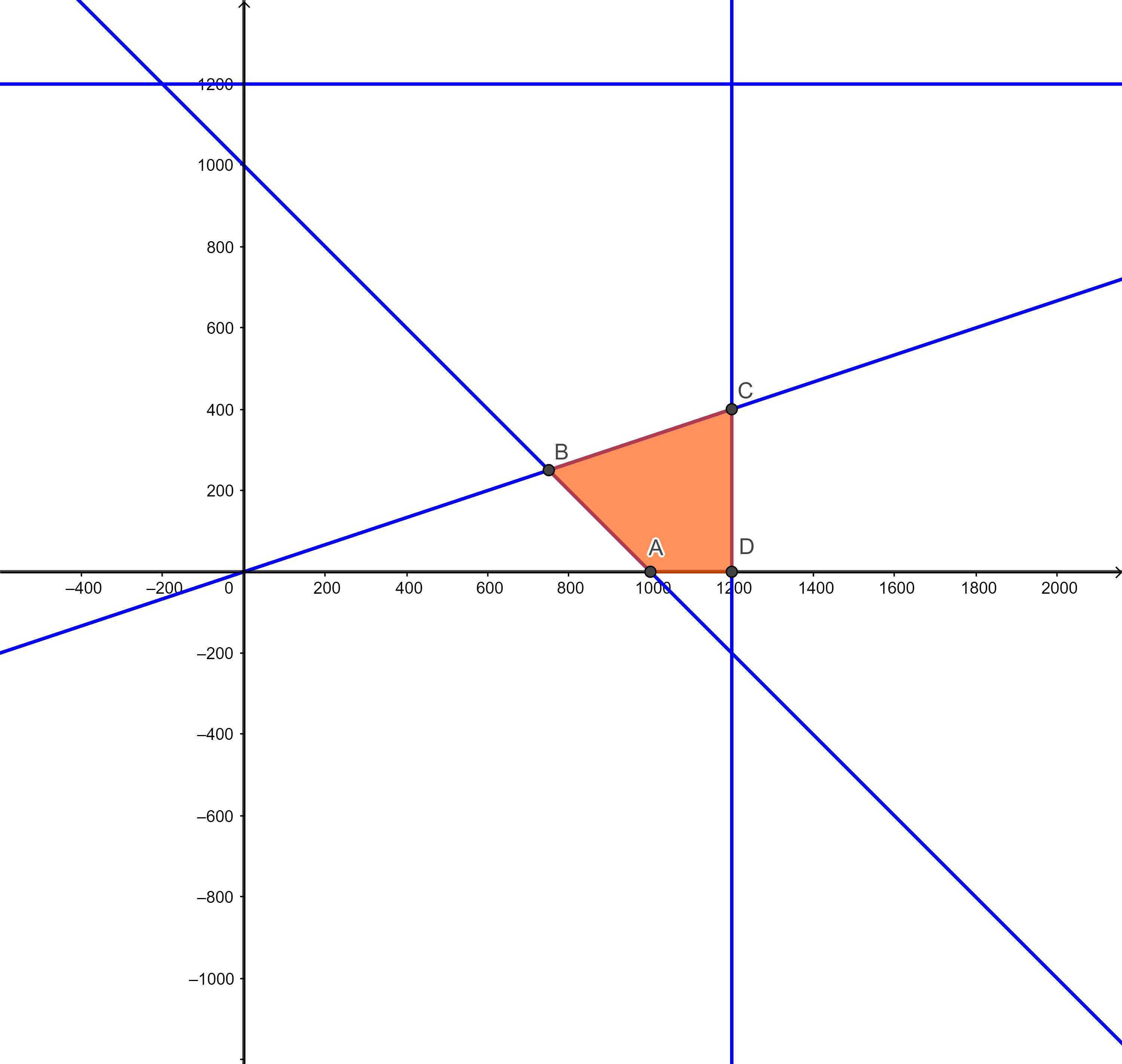
Bài 2.15 trang 32 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với tọa độ các điểm A(1 000; 0), B(750; 250), C(1 200; 400), D(1 200; 0)

Lợi nhuận bác An thu được là:

F(x;y) = 7%x + 8%y + 12%(1200 – x – y)

= 144 – 0,05x – 0,04y (triệu đồng)

Tính giá trị của F(x;y) tại các điểm A, B, C, D, ta được:

F(1 000; 0) = 144 – 0,05.1 000 – 0,04.0 = 94;

F(750; 250) = 144 – 0,05.750 – 0,04.250 = 96,5;

F(1 200 ;400) = 144 – 0,05.1 200 – 0,04.400 = 68;

F(1 200; 0) = 144 – 0,05.1 200 – 0,04.0 = 84;

=> F(x; y) lớn nhất bằng 96,5 khi x = 750, y = 250.

Vậy bác An nên đầu tư 750 trái phiếu chính phủ, 250 trái phiếu ngân hàng và 200 trái phiếu doanh nghiệp để lợi nhuận thu được là lớn nhất.

----> Câu hỏi cùng bài:

---> Bài liên quan: Giải Toán 10 Bài tập cuối chương 2 trang 31

----------------------------------------

Trên đây là lời giải chi tiết Bài 2.15 Toán lớp 10 trang 32 Bài tập cuối chương 2 trang 31 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2: Bất phương trình bậc nhất hai ẩn và hệ bất phương trình bậc nht hai ẩn. Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: