Bài 14 trang 72 SGK Toán 9 tập 2

Giải SGK Toán 9

4 Đánh giá

Toán 9 Bài 2 Liên hệ giữa cung và dây

Giải Toán 9 bài 14 Trang 72 SGK Liên hệ giữa cung và dây với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 14 trang 72 SGK Toán 9 tập 2

Bài 14 (SGK trang 72): a. Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b. Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

Hướng dẫn giải

+ Trong tam giác cân đường trung tuyến vừa là đường cao, đường phân giác, đường trung trực.

+ Điểm chính giữa cung chia cung đó thành hai cung nhỏ bằng nhau.

Lời giải chi tiết

Vẽ đường tròn tâm O bán kính R, dây cung AC

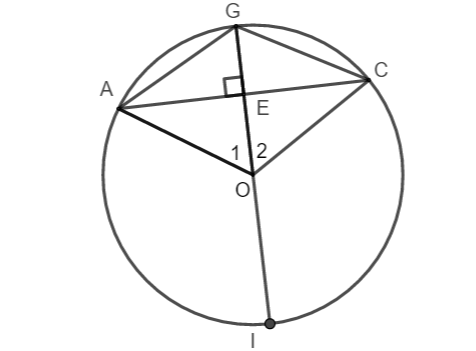
Bài 14 trang 72 SGK Toán 9 tập 2

Gọi G là điểm chính giữa cung AC, E là giao của GO và AC.

$\begin{align} & \Rightarrow \overset\frown{AG}=\overset\frown{GC}\Rightarrow sd\overset\frown{AG}=sd\overset\frown{GC} \\ & \Rightarrow \widehat{{{O}_{1}}}=\widehat{{{O}_{2}}} \\ \end{align}$

$\Rightarrow$ OG là phân giác góc O

Xét tam giác AOC có

OA = OC = R

suy tam giác AOC cân tại O

Mà OG là phân giác góc O

$\Rightarrow$ OG là trung trực, trung tuyến, đường cao của tam giác AOC

$\Rightarrow EA=EC$

Vậy đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.

Mệnh đề này sai khi dây cung trùng với đường kính.

Ví dụ: Chọn dây cung AH là một đường kính của (O). Khi đó, tồn tại đường kính EF đi qua O là trung điểm của AH nhưng E, F không phải là điểm chính giữa cung A.

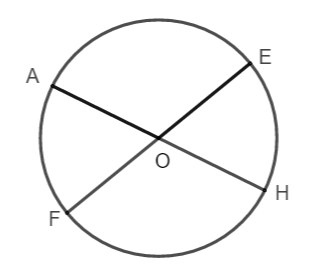
Bài 14 trang 72 SGK Toán 9 tập 2

Vậy ta cần thêm điều kiện: dây cung được chọn không phải đường kính.

b. Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy.

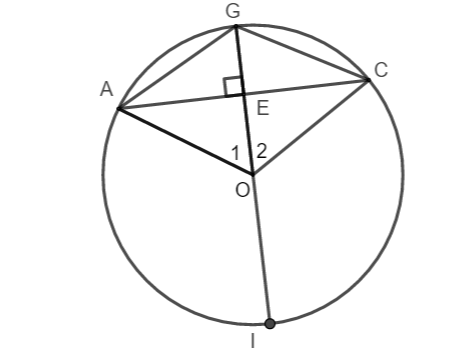
Bài 14 trang 72 SGK Toán 9 tập 2

Chứng minh tương tự câu a

Suy ra OE là đường cao của tam giác AOC

$\Rightarrow OE\bot AC$

Ngược lại: Đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.

Cho đường tròn (O) dây cung AB

Kẻ đường thẳng $OH\bot AB,\left( H\in AB \right)$ cắt đường tròn tại I

Ta có: $\Delta AOB$ cân tại O

Vậy OH vừa là đường cao, đường phân giác

$\begin{align} & \Rightarrow \widehat{AOH}=\widehat{BOH} \\ & \Rightarrow \overset\frown{AI}=\overset\frown{BI} \\ \end{align}$

Vậy I là điểm chính giữa cung AB.

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán đại 9: Liên hệ giữa cung và dây. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!