Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo Giải Toán 10 Chân trời sáng tạo

3 Đánh giá

Bài 1 trang 37 SGK Toán 10

Toán lớp 10 Bài 1 trang 37 là lời giải bài Hệ bất phương trình bậc nhất hai ẩn SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 1 Toán 10 trang 37

Bài 1 (SGK trang 37): Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:

a) $\left\{ {\begin{array}{*{20}{c}} {x + y - 3 \geqslant 0} \\ {x \geqslant 0} \\ {y \geqslant 0} \end{array}} \right.$

b) $\left\{ {\begin{array}{*{20}{c}} {x - 2y < 0} \\ {x + 3y > - 2} \\ {y - x < 3} \end{array}} \right.$

c) $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 1} \\ {x \leqslant 4} \\ {x + y - 5 \leqslant 0} \\ {y \geqslant 0} \end{array}} \right.$

Hướng dẫn giải

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết

a) Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.

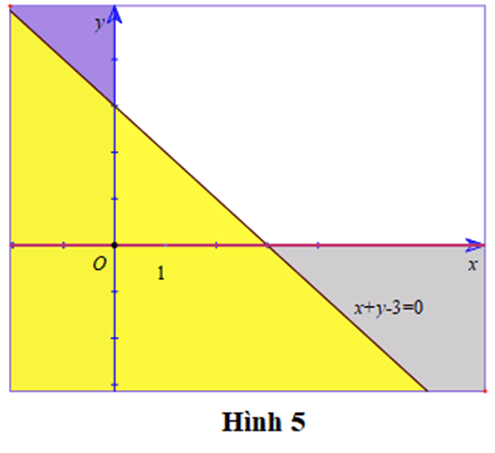
- Xác định miền nghiệm D₁của bất phương trình x + y - 3 ≥ 0:

Lấy điểm O(0; 0) không thuộc đường thẳng d: x + y – 3 = 0, ta có: 0 + 0 – 3 = -3 < 0. Do đó miền nghiệm của bất phương trình x + y - 3 ≥ 0 là nửa mặt phẳng có bờ là đường thẳng d₁(kể cả đường thẳng d₁) và không chứa gốc tọa độ O(0; 0)

- Xác định miền nghiệm D₂ của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Oy và kể cả bờ Oy

- Xác định miền nghiệm D₃của bất phương trình y ≥ 0 là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox

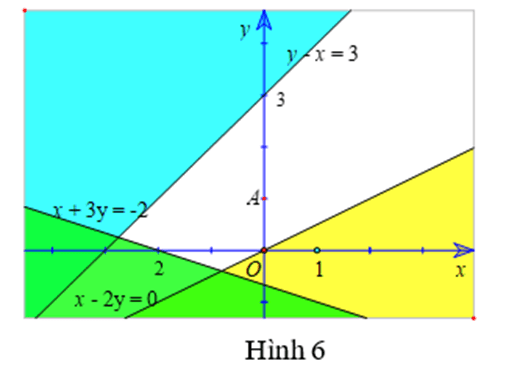
Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo

b) - Xác định miền nghiệm D₁của bất phương trình x - 2y < 0:

Lấy điểm A(0; 1) không thuộc đường thẳng d₁: x – 2y = 0, ta có: 0 – 2.1 = -2 < 0. Do đó miền nghiệm D₁là nửa mặt phẳng có bờ là đường thẳng d₁ (không kể đường thẳng d₁) và chứa điểm A (0; 1)

- Xác định miền nghiệm D₂ của bất phương trình x + 3y > -2:

Lấy điểm O(0; 0) không thuộc đường thẳng d₂: x + 3y = - 2, ta có: 0 + 3.0 = 0 > - 2. Do đó miền nghiệm D₂ là nửa mặt phẳng bờ là đường thẳng d₂(không kể đường thẳng d₂) và chứa gốc tọa độ O

- Xác định miền nghiệm D₃ của bất phương trình y – x < 3

Lấy điểm O(0; 0) không thuộc đường thẳng d₂: x + 3y = - 2, ta có: 0 + 3.0 = 0 > - 2.

Miền nghiệm của bất phương trình y – x < 3 là nửa mặt phẳng bờ là đường thẳng y – x = 3 (không kể bờ) và chứa gốc tọa độ O.

Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo

c) Biểu diễn miền nghiệm của từng bất phương trình trên mặt phẳng Oxy.

- Miền nghiệm của bất phương trình x ≥ 1 là nửa mặt phẳng kể cả bờ x = 1 và không chứa gốc tọa độ O

- Miền nghiệm của bất phương trình x ≤ 4 là nửa mặt phẳng kể cả bờ x = 4 và chứa gốc tọa độ O

- Miền nghiệm của bất phương trình x + y – 5 ≤ 0 là nửa mặt phẳng kể cả bờ x + y – 5 = 0 và chứa gốc tọa độ O (như hình 7).

- Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bên trên trục Ox và kể cả bờ Ox (như hình 7).

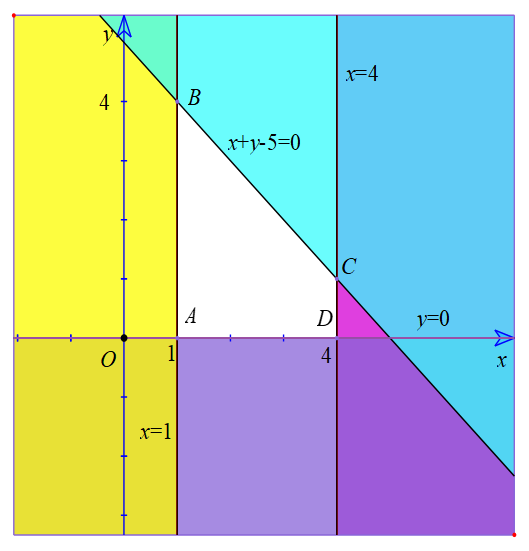
Bài 1 trang 37 Toán 10 tập 1 SGK Chân trời sáng tạo

Vậy, miền không tô màu (miền tứ giác ABCD, bao gồm cả các cạnh) trong hình 7 là phần giao các miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

----> Câu hỏi cùng bài:

------> Bài liên quan: Giải Toán 10 Bài 1 Bất phương trình bậc nhất hai ẩn

-------> Bài học tiếp theo: Giải Toán lớp 10 Bài tập cuối chương 2

----------------------------------------

Trên đây là lời giải chi tiết Bài 1 Toán lớp 10 trang 37 Hệ bất phương trình bậc nhất hai ẩn cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn . Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: