Bài 5 trang 38 Toán 10 tập 1 SGK Chân trời sáng tạo Giải Toán 10 Chân trời sáng tạo

5 Đánh giá

Bài 5 trang 38 SGK Toán 10

Toán lớp 10 Bài 5 trang 38 là lời giải bài Hệ bất phương trình bậc nhất hai ẩn SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 5 Toán 10 trang 38

Bài 5 (SGK trang 38): Trong một tuần, bạn Mạnh có thể thu xếp được tối đa 12 giờ để tập thể dục cân bằng hai môn: đạp xe và tập cử tạ tại phòng tập. Cho biết mỗi giờ đạp xe sẽ tiêu hao 350calo và không tốn chi phí, mỗi giờ tập cử tạ sẽ tiêu hao 700 calo với chi phí 50 000 đồng/ giờ. Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Hãy giúp bạn Mạnh tính số giờ xe đạp và số giờ tập tạ một tuần trong hai trường hợp sau:

a) Mạnh muốn chi phí tập luyện là thấp nhất.

b) Mạnh muốn số calo tiêu hao là nhiều nhất.

Hướng dẫn giải

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết

Gọi thời gian tập môn đạp xe của Mạnh là x (giờ)

Thời gian tập môn cử tạ của Mạng là y (giờ)

Điều kiện x ≥ 0; y ≥ 0

Do Mạnh có thể thu xếp được tối đa 12 giờ mỗi tuần để tập cả hai môn thể dục

=> x + y ≤ 12 (1)

Mỗi giờ đạp xe tiêu hao 350calo

=> x giờ đạp xe sẽ tiêu hao 350x (calo)

Mỗi giờ tập cử tạ tiêu hao 700 calo

=> y giờ tập cử tạ tiêu hao 700y (calo)

Do số calo của bạn Mạnh không vượt quá 7000 calo

=> 350x + 700y ≤ 7000

=> x + 2y ≤ 20 (2)

Ta có hệ bất phương trình: $\left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y \geqslant 0} \\ {x + y \leqslant 12} \\ {x + 2y \leqslant 20} \end{array}} \right.$

Biểu diễn miền nghiệm của bất phương trình như sau:

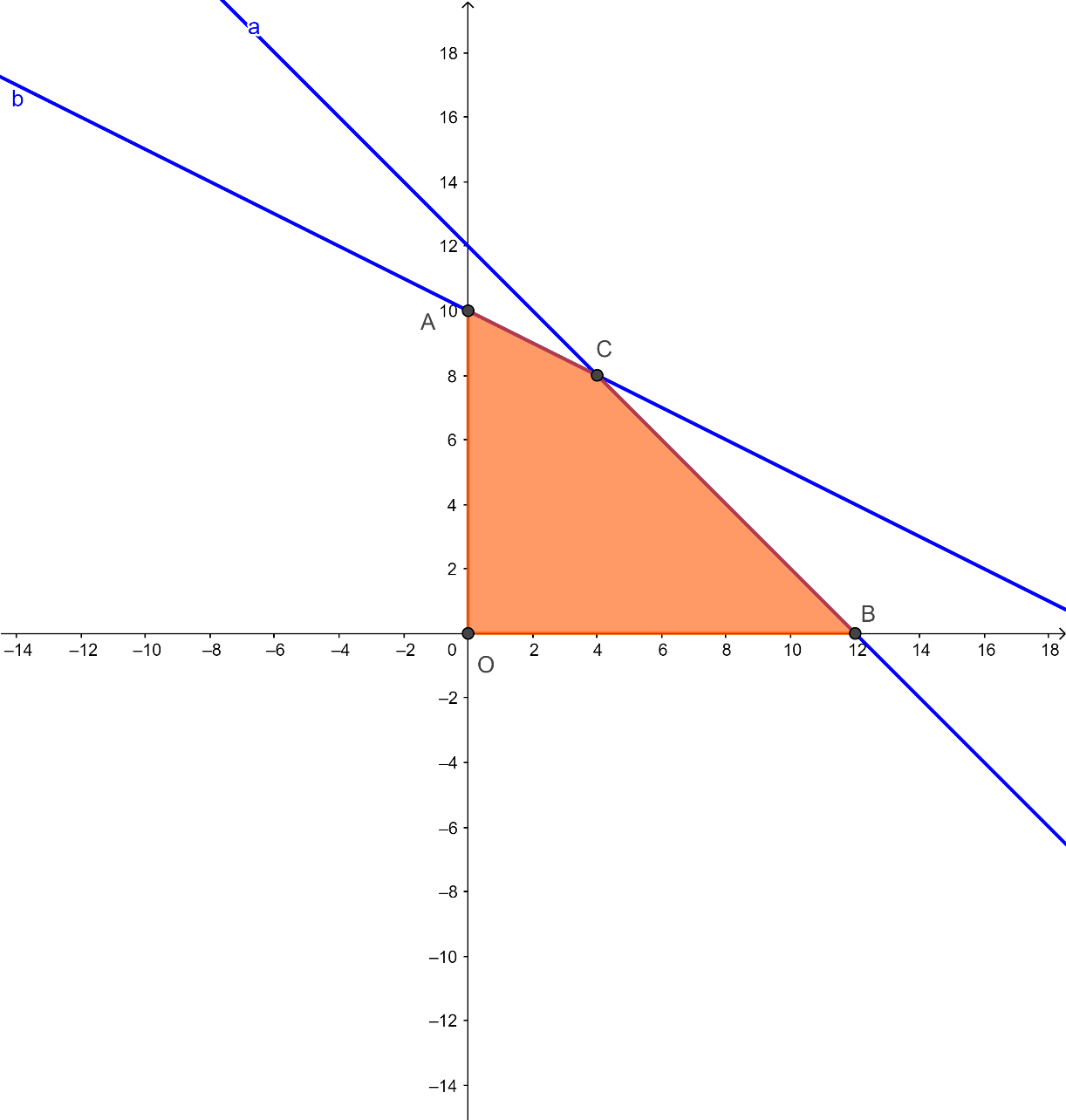
Bài 5 trang 38 Toán 10 tập 1 SGK Chân trời sáng tạo

Miền tứ giác OABC là miền nghiệm của hệ bất phương trình trên.

Ta có: Tọa độ các điểm của tứ giác là: O (0; 0); A(0; 10); B(12; 0); C(4; 8)

Mỗi giờ tập tạ có giá 50 000 đồng, đạp xe đạp không tốn phí

=> y giờ tập tạ bạn Mạnh phải trả 50 000y (đồng)

Gọi H = 50 000y

Tại điểm O (0; 0): H = 50 000 . 0 = 0

Tại điểm A(0; 10): H = 50 000 . 10 = 500 000

Tại điểm B(12; 0): H = 50 000 . 0 = 0

Tại điểm C(4; 8): H = 50 000 . 8 = 400 000

=> H đạt giá trị nhỏ nhất bằng tại O(0; 0) và B (12; 0)

Vậy Mạnh muốn chi phí tập luyện là ít khi Mạnh không tập luyện cả tuần hoặc Mạnh chỉ đạp xe 12 giờ và không tập tạ.

b) Gọi K là số calo tiêu hao

=> K = 350x + 700y

Tại điểm O (0; 0): K = 350 . 0 + 700 . 0 = 0

Tại điểm A(0; 10): K = 350 . 0 + 700 . 10 = 7000

Tại điểm B(12; 0): K = 350 . 12 + 700 . 0 = 4200

Tại điểm C(4; 8): K = 350 . 4 + 700 . 8 = 7000

=> K đạt giá trị lớn nhất bằng tại A(0; 10) và C(4; 8)

Vậy để đạt lượng calo tiêu thụ lớn nhất thì Mạnh cần tập tạ trong 10 giờ hoặc đạp xe 4 giờ kết hợp với tập tạ 8 giờ.

----> Câu hỏi cùng bài:

------> Bài liên quan: Giải Toán 10 Bài 1 Bất phương trình bậc nhất hai ẩn

-------> Bài học tiếp theo: Giải Toán lớp 10 Bài tập cuối chương 2

----------------------------------------

Trên đây là lời giải chi tiết Bài 5 Toán lớp 10 trang 38 Hệ bất phương trình bậc nhất hai ẩn cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn . Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: