Giaitoan.com Toán 7 Luyện tập Toán 7 KNTT

Chứng minh trong tam giác vuông cạnh huyền lớn hơn mỗi cạnh góc vuông Giải Toán 7

Nội dung
  • 9 Đánh giá

Quan hệ giữa góc và cạnh đối diện trong một tam giác

Mời các bạn tham khảo tài liệu Chuyên đề Tam giác vuông Toán 7 do GiaiToan.com biên soạn và đăng tải sau đây. Hy vọng đây sẽ là tài liệu hữu ích cho các em học sinh lớp 7 ôn tập và nâng cao kiến thức môn Toán 7

Chứng minh trong tam giác vuông, cạnh huyền lớn hơn mỗi cạnh góc vuông

Hướng dẫn giải

Giả sử cho tam giác ABC vuông tại A như hình vẽ:

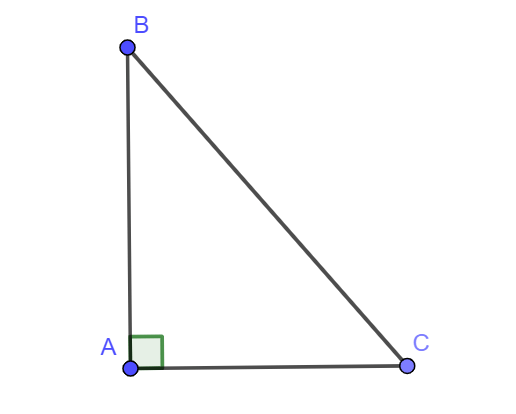
Chứng minh trong tam giác vuông cạnh huyền lớn hơn mỗi cạnh góc vuông

Xét tam giác ABC vuông tại A, ta có:

\widehat{A} +\widehat{B} +\widehat{C} = 180^{\circ}(tổng ba góc trong một tam giác bằng 1800)

⇒ \widehat{B} +\widehat{C}=180^{\circ} -\widehat{A}= 1800 – 900 = 900

⇒ \left\{\begin{matrix} \widehat{B} < 90^{\circ} \\ \widehat{C} < 90^{\circ} \end{matrix}\right.

• Trong tam giác vuông thì góc vuông là góc có số đo lớn nhất và cạnh đối diện với góc lớn hơn thì lớn hơn

Mà cạnh huyền đối diện với góc vuông (là góc lớn nhất)

⇒ AB < BC và AC < BC

Vậy trong tam giác vuông cạnh huyền lớn hơn mỗi cạnh góc vuông.

Góc đối diện với cạnh lớn hơn

• Định lý: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn

Cạnh đối diện với góc lớn hơn

• Định lý: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn

• Đối với tam giác tù: Cạnh đối diện với góc tù là cạnh lớn nhất

• Đối với tam giác vuông: Cạnh huyền đối diện với góc vuông nên cạnh huyền là cạnh lớn nhất.

• Đối với tam giác cân: Hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau

• Đối với tam giác đều: Ba cạnh của tam giác bằng nhau, ba góc bằng nhau

– – – – – – – – – – – – –

Chia sẻ bởi: Thiên Bình
Mời bạn đánh giá!
  • Lượt xem: 6.199
Tìm thêm: Toán 7 chuyên đề toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần