Bài 37 trang 79 SGK Toán 8 tập 2

Giải SGK Toán 8

1 Đánh giá

Toán 8 Bài 7: Trường hợp đồng dạng thứ ba

Bài 37 trang 79 SGK Toán 8 tập 2 biên soạn và đăng tải với hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Bài 37 Trang 79 SGK Toán 8 - Tập 2

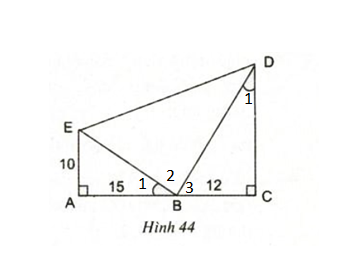
Bài 37 (SGK trang 79): Hình 44 cho biết góc EBA bằng góc BDC.

a) Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích của hai tam giác AEB và BCD.

Bài 37 trang 79 SGK Toán 8 tập 2

Hướng dẫn giải

Nếu hai góc tam giác này bằng với hai góc của tam giác kia thì hai tam giác đồng dạng sử dụng tỉ số đồng dạng của tam giác.

Lời giải chi tiết

Bài 37 trang 79 SGK Toán 8 tập 2

a) Ta có: $\left\{ {\begin{array}{*{20}{c}} {\widehat {{B_3}} + \widehat {{D_1}} = {{90}^0}} \\ {\widehat {{B_1}} = \widehat {{D_1}}} \end{array}} \right. \Rightarrow \widehat {{B_3}} + \widehat {{B_1}} = {90^0} \Rightarrow \widehat {{B_2}} = {90^0}$

Vậy ΔBED vuông tại B.

b) Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:

$\begin{matrix} B{E^2} = A{E^2} + A{B^2} = {10^2} + {15^2} = 325 \hfill \\ \Rightarrow BE \approx 18cm \hfill \\ \end{matrix}$

Xét tam giác $\Delta ABE$ và $\Delta DCB$ có:

$\left\{ {\begin{array}{*{20}{c}} {\widehat A = \widehat C = {{90}^0}} \\ {\widehat {{B_1}} = \widehat {{D_1}}} \end{array}} \right. \Rightarrow \Delta ABE \sim \Delta DCB\left( {g - g} \right)$

$\begin{matrix} \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{BE}}{{BD}} = \dfrac{{EA}}{{BC}} \hfill \\ \Rightarrow \dfrac{{15}}{{CD}} = \dfrac{{18}}{{BD}} = \dfrac{{10}}{{12}} \hfill \\ \Rightarrow DC = 18;DB \approx 21,6 \hfill \\ \end{matrix}$

Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:

$D{E^2} = B{E^2} + B{D^2} = {18^2} + 21,{6^2} \Rightarrow DE \approx 28,2$

${S_{ABE}} = \frac{1}{2}AE.AB = \frac{1}{2}.10.15 = 75$

${S_{BDE}} = \frac{1}{2}.BE.BD = \frac{1}{2}.18.21,6 = 194,4$

$\Rightarrow {S_{ABE}} + {S_{BCD}} = 75 + 108 < {S_{BDE}}$

_{-------------------------------------------------------------}

Trên đây là lời giải chi tiết bài tập Toán 8 bài 7: Trường hợp đồng dạng thứ ba cho các em học sinh tham khảo, nắm được cách giải các dạng toán Chương 3: Tam giác đồng dạng Toán 8 Tập 2. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 8. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!