Bài 30 trang 79 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 4 Góc tạo bởi tia tiếp tuyến và dây cung

Giải Toán 9 bài 30 Trang 79 SGK Góc tạo bởi tia tiếp tuyến và dây cung với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 30 trang 79 SGK Toán 9 tập 2

Bài 30 (SGK trang 79): Chứng minh định lí đảo của định lý về góc tạo bởi tia tiếp tuyến và dây cung, cụ thể là:

Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn (h.29).

Bài 30 trang 79 SGK Toán 9 tập 2

Gợi ý: Có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.

Hướng dẫn giải

- Trong một đường tròn, góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì có số đo bằng nhau và bằng nửa số đo cung bị chắn.

Lời giải chi tiết

Cách 1: Chứng minh trực tiếp

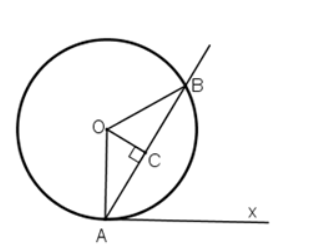
Bài 30 trang 79 SGK Toán 9 tập 2

Gọi C là chân đường cao hạ từ C xuống AB

Tam giác ABO cân tại O nên đường cao CO đồng thời là đường phân giác

$\Rightarrow \widehat{AOC}=\frac{1}{2}\widehat{AOB}$

Mặt khác $\widehat{BAx}=\frac{1}{2}sd\overset\frown{AB};\widehat{AOB}=\frac{1}{2}sd\overset\frown{AB}$

$\begin{align} & \Rightarrow \widehat{BAx}=\frac{1}{2}\widehat{AOB} \\ & \Rightarrow \widehat{BAx}=\widehat{AOC} \\ & \Rightarrow \widehat{OAx}=\widehat{BAO}+\widehat{BAx}=\widehat{BAO}+\widehat{AOC}={{90}^{0}} \\ & \Rightarrow OA\bot Ax \\ \end{align}$

Vậy Ax là tiếp tuyến của (O) tại A.

Cách 2: Chứng minh gián tiếp

Giả sử Ax không phải tiếp tuyến của (O)

Suy ra Ax cắt (O) tại C khác A.

Trường hợp 1: C nằm trên cung nhỏ AB

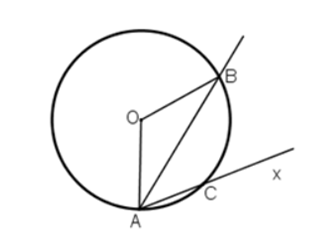
Bài 30 trang 79 SGK Toán 9 tập 2

$\Rightarrow \widehat{BAx}=\widehat{BAC}$ (cùng chắn cung BC)

$\Rightarrow \widehat{BAx}=\frac{1}{2}sd\overset\frown{AC}$

Mà $sd\overset\frown{AC}< sd\overset\frown{AB}\Rightarrow \widehat{BAx}< \frac{1}{2}sd\overset\frown{Ab}$

Ngược lại với đề bài

Trường hợp 2: C nằm trên cung lớn AB

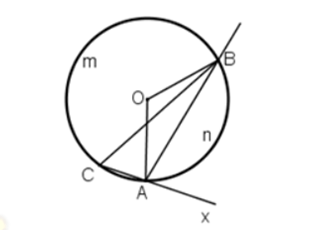
Bài 30 trang 79 SGK Toán 9 tập 2

$\Rightarrow \widehat{BAC}$ là góc nội tiếp chắn cung AnB

$\Rightarrow \widehat{BCA}=\frac{1}{2}sd\overset\frown{BnA}$

Mà $\widehat{BAx}$ là góc ngoài tam giác ABC

$\begin{align} & \Rightarrow \widehat{BAx}>\widehat{BCA} \\ & \Rightarrow \widehat{BAx}>\frac{1}{2}sd\overset\frown{BnA} \\ \end{align}$

Ngược lại với đề bài

Vậy Ax là tiếp tuyến đường tròn tâm O.

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Góc tạo bởi tia tiếp tuyến và dây cung. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!