Bài 3 trang 107 Toán 7 tập 2 SGK Cánh Diều Giải Toán 7 Cánh Diều

Bài 3 trang 107 SGK Toán 7 tập 2

Bài 3 trang 107 Toán 7 tập 2 SGK CD thuộc bài 10: Tính chất ba đường trung tuyến của tam giác được hướng dẫn chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7.

Giải Bài 3 Toán 7 tập 2 SGK trang 107

Bài 3 (SGK trang 107): Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:

a) GA = GD;

b) ∆MBG = ∆MCD;

c) CD = 2GN.

Lời giải:

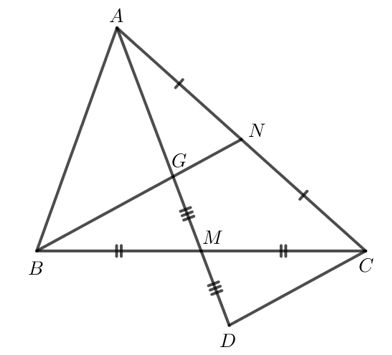
a) Tam giác ABC có hai đường trung tuyến AM, BN cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Khi đó

Trên tia đối của tia MA lấy điểm D sao cho MD = MG nên M là trung điểm của GD.

Suy ra

Vậy GA = GD.

b) Do M là trung điểm của GD nên MG = MD.

Xét ∆MBG và ∆MCD có:

MB = MC (theo giả thiết).

(2 góc đối đỉnh).

MG = MD (chứng minh trên).

Do đó ∆MBG = ∆MCD (c - g - c).

c) Do ∆MBG = ∆MCD (c - g - c) nên CD = BG (2 cạnh tương ứng).

Do G là trọng tâm của tam giác ABC nên BG = 2GN.

Mà CD = BG nên CD = 2GN.

Câu hỏi trong bài: Giải Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Câu hỏi cùng bài:

• Bài 2 (SGK trang 107): Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN...
• Bài 4 (SGK trang 107): Cho tam giác ABC có hai đường trung tuyến AM và BN....
• Bài 5 (SGK trang 107): Hình 107 là mặt cắt đứng của một ngôi nhà có mái dốc....

Bài tiếp theo: Giải Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

Trên đây là lời giải Bài 3 trang 107 Toán 7 tập 2 SGK Cánh Diều chi tiết cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 7: Tam giác. Nhằm giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7 đạt kết quả cao, GiaiToan mời các bạn tham khảo thêm chuyên mục SGK Toán 7 sách Cánh Diều. Chúc các em học tốt. Mời thầy cô và học sinh tham khảo thêm tài liệu: Giải Toán 7 tập 2 KNTT, Giải Toán 7 Chân trời sáng tạo tập 2.