Bài 1.13 trang 19 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 2

Bài 1.13 trang 19 Toán 12 KNTT

Toán 12 Bài 1.13 trang 19 Tập 1 là câu hỏi trong bài Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số với lời giải chi tiết giúp cho các em học sinh tham khảo, củng cố kỹ năng giải Toán 12 KNTT.

Giải Bài 1.13 Toán 12 trang 19

Lời giải chi tiết:

Nửa chu vi là: 24 : 2 = 12 cm

Gọi chiều dài là x (cm), chiều rộng là 12 - x (cm) (0 < x < 12)

Gọi S(x) là hàm số biểu thị diện tích của hình chữ nhật, ta có:

S(x) = x(12 - x) = 12x - x², 0 < x < 12

Ta có: S'(x) = 12 - 2x; S'(x) = 0 ⇔ x = 6

Lập bảng biến thiên của hàm số S(x) trên (0; 12):

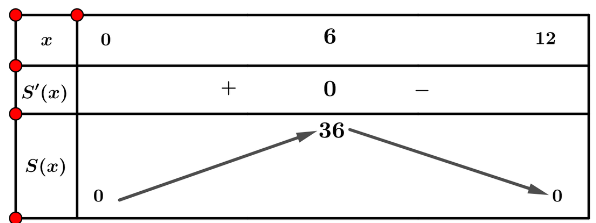
Từ bảng biến thiên, ta có

Vậy hình chữ nhật có diện tích lớn nhất là 36 cm² (tức là khi chữ nhật trở thành hình vuông)

---> Câu hỏi cùng bài:

• Bài 1.11 trang 19 toán 12 tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có)
• Bài 1.12 trang 19 toán 12 tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
• Bài 1.14 trang 19 toán 12 tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp
• Bài 1.15 trang 19 toán 12 tập 1: Một nhà sản xuất cần làm ra những chiếc bình có dạng

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài 3: Đường tiệm cận của đồ thị hàm số