Trực tâm là gì? Cách xác định trực tâm Bài tập Toán 7

Chuyên đề Toán 7: Tam giác

Chắc hẳn các bạn học sinh đôi lúc sẽ gặp khó khăn với các câu hỏi Trực tâm là gì? Xác định được trực tâm tam giác bằng cách nào?. Để trả lời cho các câu hỏi đó GiaiToan.com xin giới thiệu đến bạn đọc tài liệu Trực tâm tam giác gồm các kiến thức trọng tâm và trực quan giúp học sinh dễ hiểu, dễ nhớ, áp dụng vào làm bài tập tốt. Hy vọng đây sẽ là tài liệu hữu ích cho các em học sinh lớp 7 ôn tập và nâng cao kiến thức môn Toán 7.

A. Trực tâm

- Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác

Hay nói cách khác:

- Trực tâm là giao của ba đường cao trong tam giác.

Hình vẽ minh họa:

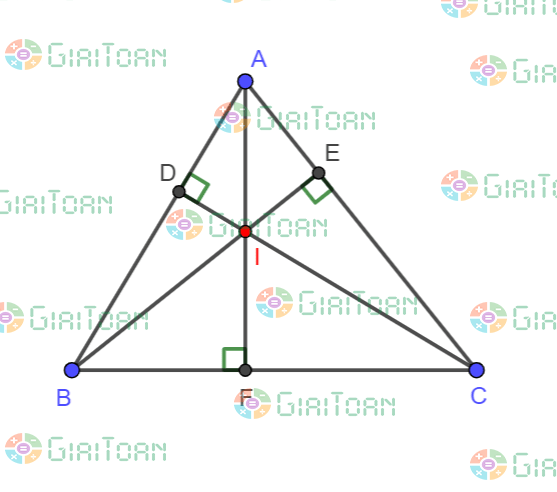
Trong hình vẽ trên, các đoạn thẳng AF, CD, BE lần lượt là các đường cao hạ từ A, C, B của tam giác ABC. Điểm I là giao điểm của ba đường cao

=> Điểm I là trực tâm của tam giác.

Chú ý: Trong tam giác đều, trực tâm cách đều ba cạnh của tam giác

B. Cách xác định trực tâm tam giác

Phương pháp: Để xác định trực tâm tam giác, ta đi tìm giao điểm của hai đường cao trong tam giác đó.

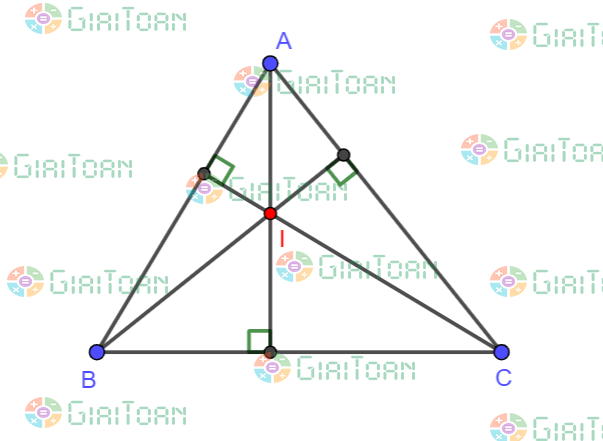
Hướng dẫn giải

Vì I là trực tâm của tam giác ABC

=> AI ⊥ BC, BI ⊥ AC, CI ⊥ AB

Xét tam giác IAB có BC ⊥ AI, AC ⊥ BI

=> Điểm C là giao điểm của BC và AC

=> Điểm C là trực tâm tam giác IAB

Chứng minh tương tự ta có B là trực tâm tam giác IAC, A là trực tâm tam giác IBC.

Hướng dẫn giải

Xét bài toán phụ nếu tam giác ABC có M, N lần lượt là trung điểm của AB và AC thì MN // BC và BC = 2MN.

Thật vậy, trên tia đối của tia NM lấy điểm P sao cho NP = MN

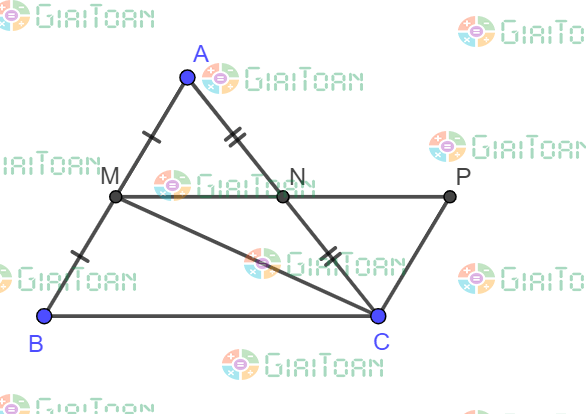
Xét tam giác AMN và tam giác CPN có

AM = NC

(đối đỉnh)

MN = NP

=> ∆AMN = ∆ CPN (c – g – c)

=> MA = CP, (hai cạnh và hai góc tương ứng)

Hai góc ở vị trí so le trong nên AM // CP

=> (hai góc so le trong)

Xét tam giác BMC và tam giác PCM có

MB = CP = MA

(cmt)

MC là cạnh chung

=> ∆BMC = ∆PCM (c – g – c)

=> BC = NP, (cặp cạnh và góc tương ứng)

Hai góc ở vị trí so le trong nên MN // BC

Ta lại có MP = MN + NP = 2MN

=> BC = 2MN

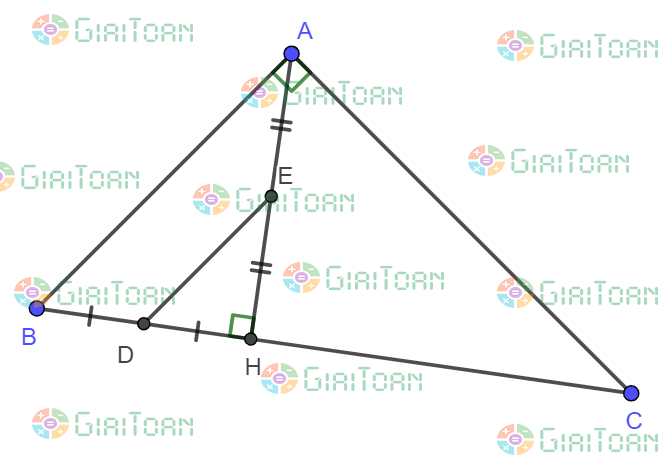
Xét tam giác HAB có:

BD = DH

EA = EH

=> DE // AB (theo chứng minh bên trên)

Xét tam giác ADE có

CD ⊥ AE mặt khác CA ⊥ AB và DE // AB

=> CA ⊥ DE

=> CA, DC là đường cao của tam giác ADE

Mà C là giao điểm của AC và DC

=> C là trực tâm của tam giác ADE

C. Bài tập xác định trực tâm của tam giác

Bài tập 1: Cho tam giác ABC có M là trung điểm của BC và MA = MB = MC. Tìm trực tâm của tam giác ABC.

Bài tập 2: Cho tam giác ABC có góc A bằng 70⁰, AB < AC, đường phân giác góc A cắt BC tại D, BF ⊥ AC tại E, F thuộc AC sao cho AE = AB. Xác định trực tâm tam giác ABE và tính số đo góc DHF.

-------------------------------------------------------

Hy vọng tài liệu trên sẽ giúp các em học sinh ghi nhớ lý thuyết về tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng hơn. Chúc các em học tốt.