Tính chất ba đường trung trực của tam giác Đường trung trực

Bài tập Toán 7: Tính chất đường trung trực

Chắc hẳn các bạn học sinh đôi lúc sẽ gặp khó khăn với các câu hỏi Đường trung trực là gì? Tính chất đường trung trực, ứng dụng tính chất đường trung trực trong giải tam giác. Để trả lời cho các câu hỏi đó GiaiToan.com xin giới thiệu đến bạn đọc tài liệu Tính chất đường trung trực gồm các kiến thức trọng tâm và trực quan giúp học sinh dễ hiểu, dễ nhớ, áp dụng vào làm bài tập tốt. Hy vọng đây sẽ là tài liệu hữu ích cho các em học sinh lớp 7 ôn tập và nâng cao kiến thức môn Toán 7.

A. Tính chất 3 đường trung trực của tam giác

- Trong một tam giác, đường trung trực của một cạnh được gọi là một đường trung trực của tam giác đó.

+ Ba đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó. Điểm này chính là tâm đường tròn đi qua 3 đỉnh của tam giác (ta gọi đường tròn này là đường tròn ngoại tiếp tam giác)

B. Tính chất đường trung trực

+ Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường trung tuyến, đường phân giác xuất phát từ đỉnh đối diện.

+ Trong một tam giác, nếu hai trong ba đường (đường trung tuyến, đường phân giã xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó cân.

C. Bài tập tính chất ba đường trung trực của tam giác

Hướng dẫn giải

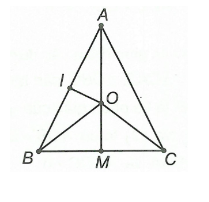
Xét tam giác OAB vì OI là trung trực của AB => OA = OB

Vì tam giác ABC cân tại A nên đường trung tuyến AM đồng thời là đường trung trực của BC

Mà đường trung trực của AB cắt AM tại O nên O là giao điểm của 3 đường trung trực.

Vậy O cách đều ba đỉnh của tam giác ABC.

Hướng dẫn giải

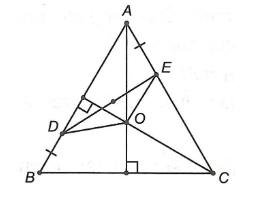
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC

=> OA = OB = OC

Ta có AO là đường trung trực ứng với cạnh BC đồng thời là đường phân giác trong của góc A.

=>

Tương tự ta có:

Vì tam giác ABC là tam giác đều nên AB = AC = BC

Ta lại có:

Xét tam giác OAD và tam giác OCE có:

OA = OC

CE = AD

=> OD = OE

=> Tam giác ODE cân tại O

Vậy đường trung trực của đoạn DE luôn đi qua điểm cố định O.

Hướng dẫn giải

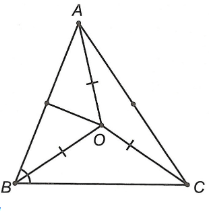
Vì O là giao điểm của các đường trung trực của tam giác ABC

=> OA = OB = OC

=> Tam giác OAB và tam giác OBC cân tại O

=> (*)

Do OB là tia phân giác của góc nên (**)

Từ (1) và (2) ta có:

Xét tam giác BOA và BOC ta có:

OA = OC

OB chung

b) VÌ => AB = BC (hai cạnh tương ứng)

=> Tam giác BAC cân tại B

Mà OB là tia phân giác của góc ABC nên OB là đường trung trực của AC.

---------------------------------------------

Hy vọng tài liệu Bài tập tính chất đường trung trực Toán 7 sẽ giúp các em học sinh củng cố, ghi nhớ lý thuyết, bài tập Làm quen với số liệu thống kê. từ đó vận dụng giải các bài toán Toán lớp 7 một cách dễ dàng, chuẩn bị hành trang kiến thức vững chắc trong năm học lớp 7. Chúc các em học tốt.