Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Luyện tập 2 trang 38 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 5

Nội dung
  • 1 Đánh giá

Luyện tập 2 trang 38 Toán 12 KNTT

Toán 12 Luyện tập 2 trang 38 Tập 1 là câu hỏi trong bài Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn với lời giải chi tiết giúp cho các em học sinh tham khảo, củng cố kỹ năng giải Toán 12 Kết nối tri thức.

Giải Luyện tập 2 Toán 12 trang 38

Luyện tập 2 trang 38 toán 12 tập 1: Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3 km và muốn đến điểm B ở bờ đối diện cách 8 km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyền thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6 km/h và vận tốc chạy bộ là 8 km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến được B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).

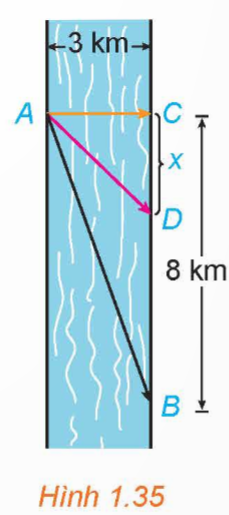
Lời giải chi tiết:

Gọi x (km) là quãng đường từ C đến D (x > 0)

Quãng đường AD là: \sqrt{x^2+9} (km)

Quãng đường BD là: 8 - x (km)

Thời gian anh An chèo thuyền từ A đến D là: \frac{\sqrt{x^2+9}}{6} (giờ)

Thời gian anh An chạy bộ từ D đến B là: \frac{\sqrt{x^2+9}}{6} (giờ)

Tổng thời gian anh An chèo thuyền đến một điểm D giữa C và B rồi chạy bộ đến B là:

T=\frac{\sqrt{x^2+9}}{6}+\frac{8-x}{8}, \ x > 0

Ta có:

T'=\frac{x}{6\sqrt{x^2+9}}-\frac{1}{8} , \ T'=0\Leftrightarrow x=\frac{9}{\sqrt{7} }

Bảng biến thiên:

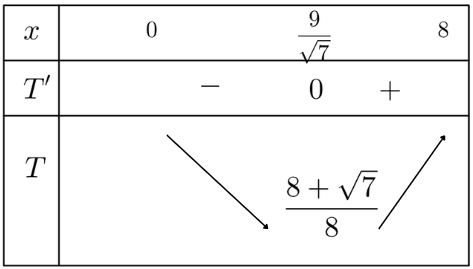
Khi đó anh An chèo thuyền đến một điểm D giữa C và B, cách C một khoảng \frac{9}{\sqrt{7}} thì đến B sớm nhất.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài tập cuối chương 1

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 31
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần