Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Luyện tập 1 trang 17 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 2

Nội dung
  • 1 Đánh giá

Luyện tập 1 trang 17 Toán 12 KNTT

Toán 12 Luyện tập 1 trang 17 Tập 1 là câu hỏi trong bài Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sách Kết nối tri thức lời giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 12 KNTT. Mời các em học sinh cùng tham khảo chi tiết.

Giải Luyện tập 1 Toán 12 trang 17

Luyện tập 1 trang 17 toán 12 tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y=\sqrt{2x-x^2}

b) y=-x+\frac{1}{x-1} trên khoảng (1; +∞)

Lời giải chi tiết:

a) y=\sqrt{2x-x^2}

Tập xác định của hàm số là: [0; 2]

Ta có: 

  • y=\sqrt{2x-x^2} \ge0; dấu bằng xảy ra khi 2x - x2 = 0, tức là khi x = 0 hoặc x = 2.

Do đó \underset{[-1;1]}{min} \ y= y(0) = y(2) = 0.

  • y=\sqrt{2x-x^2} \le0; dấu bằng xảy ra khi 2x - x2 = 1, tức là x = 1.

Do đó \underset{[-1;1]}{max} \ y= y(1) = 1

b) y=-x+\frac{1}{x-1} trên khoảng (1; +∞)

Với x ∈ (1; +∞), ta có: y'=-1-\frac{1}{\left(x-1\right)^2} <0

Tính các giới hạn:

\lim_{x\rightarrow 1^+} y=\lim_{x\rightarrow 1^+} \left ( -x+\frac{1}{x - 1} \right ) =+ \infty 

\lim_{x\rightarrow +\infty } y=\lim_{x\rightarrow +\infty } \left ( -x+\frac{1}{x - 1} \right ) = - \infty

Lập bảng biến thiên của hàm số trên khoảng (1; +∞):

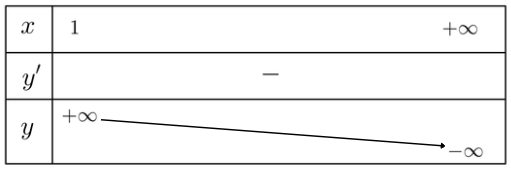
Từ bảng biến thiên, hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài 3: Đường tiệm cận của đồ thị hàm số

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 319
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

Chủ đề liên quan

Mới nhất trong tuần