Bài 63 trang 92 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 8 Đường tròn ngoại tiếp. Đường tròn nội tiếp

Giải Toán 9 Bài 63 Trang 92 SGK Đường tròn ngoại tiếp. Đường tròn nội tiếp với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 63 trang 92 SGK Toán 9 tập 2

Bài 63 (SGK trang 92): Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nột tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.

Hướng dẫn giải

- Muốn vẽ đường tròn ngoại tiếp đa giác trước hết ta phải xác định tâm đường tròn ngoại tiếp một đa giác bằng cách tìm một điểm thuộc đa giác sao cho điểm đó cách đều tất cả các đỉnh của đa giác đó.

Lời giải chi tiết

Hình lục giác đều

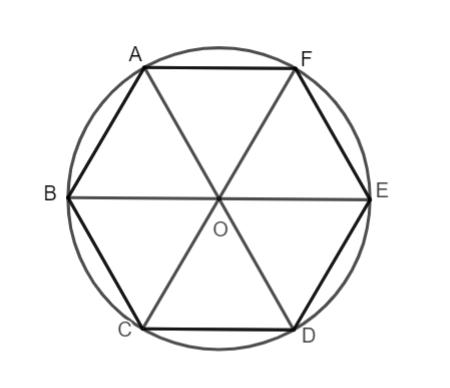
Bài 63 trang 92 SGK Toán 9 tập 2

Cách dựng hình

+ Lấy điểm A trên (O ; R).

+ Vẽ cung tròn (A; R) cắt (O; R) tại B và F => AB = AF = R

+ Vẽ cung tròn (B; R) cắt (O; R) tại C (khác A) => BC = R

+ Vẽ cung tròn (C; R) cắt (O; R) tại D (khác B) => CD = R

+ Vẽ cung tròn (D; R) cắt (O; R) tại E (khác C)=> DE = R

ABCDEF là lục giác đều cần vẽ.

Tính cạnh của tam giác đều: AB = BC = CD = DE = EF = FA = R.

Hình vuông

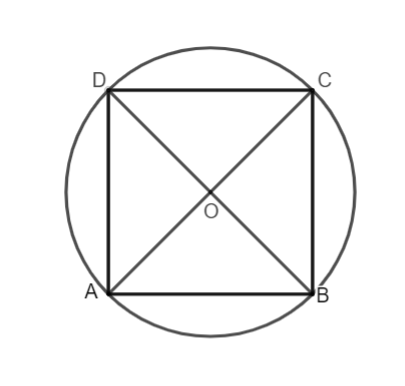
Bài 63 trang 92 SGK Toán 9 tập 2

Cách dựng hình:

- Vẽ đường kính AC của đường tròn tâm O.

- Vẽ đường kính BD ⊥ AC

Hình vuông ABCD là tứ giác có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.

Nối A với B; B với C; C với D với A ta được hình vuông ABCD nội tiếp đường tròn (O).

Tính cạnh hình vuông

Xét ΔOCD vuông tại O có OC = OD = R, áp dụng định lí Pi – ta – go cho tam giác vuông ta có:

$C{D^2} = O{C^2} + O{D^2} \Rightarrow CD = \sqrt {O{C^2} + O{D^2}} = \sqrt {{R^2} + {R^2}} = \sqrt {2{R^2}} = R\sqrt 2$

Suy ra AB = BC = CD = DA = $R\sqrt 2$

Tam giác đều

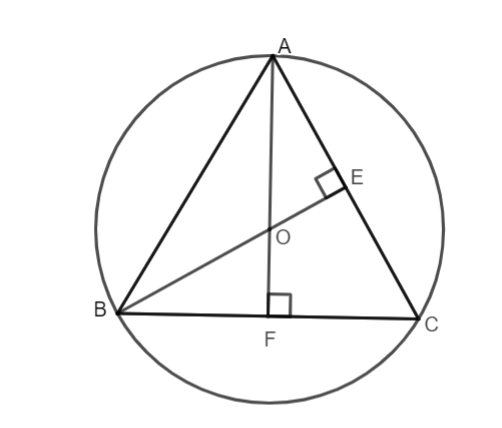
Bài 63 trang 92 SGK Toán 9 tập 2

Cách dựng hình:

Làm tương tự như câu a rồi nối các điểm ta được tam giác đều.

Tính cạnh của tam giác đều

Gọi cạnh ΔABC đều là a.

Gọi F là trung điểm BC

$\Rightarrow FB = \frac{a}{2} \Rightarrow AF = \sqrt {A{B^2} - B{F^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}$

Tam giác ABC là tam giác đều có O là tâm đường tròn ngoại tiếp đồng thời là trọng tâm tam giác

$\begin{matrix} \Rightarrow AF = \dfrac{{3.OA}}{2} \hfill \\ \Rightarrow \dfrac{{a\sqrt 3 }}{2} = \dfrac{3}{2}.R \hfill \\ \Rightarrow a = \dfrac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \hfill \\ \end{matrix}$

------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Đường tròn ngoại tiếp. Đường tròn nội tiếp. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!