Bài 61 trang 91 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 8 Đường tròn ngoại tiếp. Đường tròn nội tiếp

Giải Toán 9 Bài 61 Trang 91 SGK Đường tròn ngoại tiếp. Đường tròn nội tiếp với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 61 trang 91 SGK Toán 9 tập 2

Bài 61 (SGK trang 91):

a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).

Lời giải chi tiết

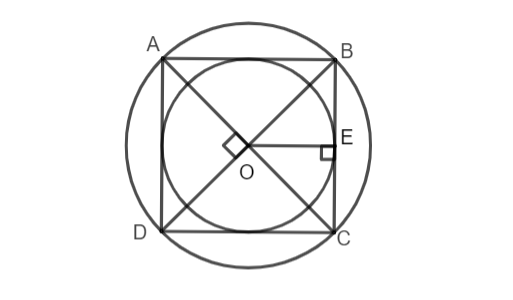
Bài 61 trang 91 SGK Toán 9 tập 2

a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O ta được đường tròn tâm O bán kính 2cm.

b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).

c) Vẽ OH ⊥ BC.

⇒ OE là khoảng cách từ từ tâm O đến BC

Vì AB = BC = CD = DA (ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau (định lý giữa dây cung và khoảng cách từ tâm đến dây)

⇒ O là tâm đường tròn nội tiếp hình vuông ABCD

OE là bán kính r của đường tròn nội tiếp hình vuông ABCD.

Tam giác vuông OBC có OE là đường trung tuyến $\Rightarrow EO = \frac{1}{2}BC = BE$

Xét tam giác vuông OEB, áp dụng định lí Pi – ta – go cho tam giác vuông ta có:

$O{E^2} + E{B^2} = O{B^2} \Rightarrow 2{r^2} = {2^2} \Rightarrow {r^2} = 2 \Rightarrow r = \sqrt 2 \left( {cm} \right)$

Vẽ đường tròn (O; OE). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Đường tròn ngoại tiếp. Đường tròn nội tiếp. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!