Giaitoan.com Toán 7 Giải Toán 7 CTST - Tập 2

Bài 5 trang 76 Toán 7 tập 2 SGK Chân trời sáng tạo Giải Toán 7 Chân trời sáng tạo

Nội dung
  • 1 Đánh giá

Bài 5 trang 76 SGK Toán 7 tập 2

GiaiToan mời các bạn cùng theo dõi lời giải Bài 5 trang 76 Toán lớp 7 tập 2 thuộc bài 7 Tính chất ba đường trung tuyến của tam giác được hướng dẫn chi tiết dưới đây giúp cho các em học sinh ôn tập, củng cố kỹ năng giải Toán 7 nhằm chuẩn bị cho các bài kiểm tra đạt kết quả cao.

Giải Bài 5 Toán 7 tập 2 SGK trang 76

Bài 5 (SGK trang 76): Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Lời giải:

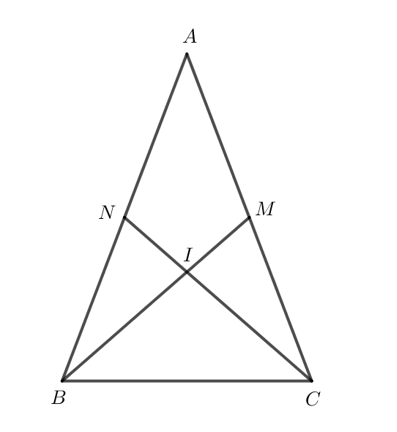
Bài 5 trang 76 Toán 7 Tập 2 Chân trời sáng tạo

Gọi giao điểm của BM và CN là I.

Tam giác ABC có I là giao điểm hai đường trung tuyến nên I là trọng tâm của tam giác ABC.

Khi đó BI = \frac{2}{3} BM , IM = \frac{1}{3} BM, CI = \frac{2}{3} CN, IN = \frac{1}{3} CN

Mà BM = CN nên BI = CI, IM = IN.

Xét Δ NIB và Δ MIC có:

IN = IM (chứng minh trên).

\hat{NIB} = \hat{MIC} (đối đỉnh).

IB = IC (chứng minh trên).

Do đó Δ NIB = Δ MIC (c.g.c).

Suy ra BN = CM (2 cạnh tương ứng).

Do BM và CN là các đường trung tuyến của tam giác ABC nên M và N lần lượt là trung điểm của AC và AB.

Suy ra BN = \frac{1}{2} AB, CM = \frac{1}{2} AC

Do đó AB = AC.

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Câu hỏi trong bài: Giải Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác

Câu hỏi cùng bài:

Bài 5 trang 76 Toán 7 tập 2 SGK CTST được GiaiToan đăng tải lời giải chi tiết cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 8: Tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7 đạt kết quả cao. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm các câu hỏi, bài tập hay bài học khác trong chuyên mục Toán 7 sách Chân trời sáng tạo.

Chia sẻ bởi: nguyen hoang thu cuc
Mời bạn đánh giá!
  • Lượt xem: 386
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần