Bài 42 trang 121 SGK Toán 8 tập 2

Giải SGK Toán 8

2 Đánh giá

Toán 8 Bài 8 Diện tích xung quanh của hình chóp đều

Bài 42 Trang 121 SGK Toán 8 tập 2 biên soạn và đăng tải với hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Bài 42 Trang 121 SGK Toán 8 - Tập 2

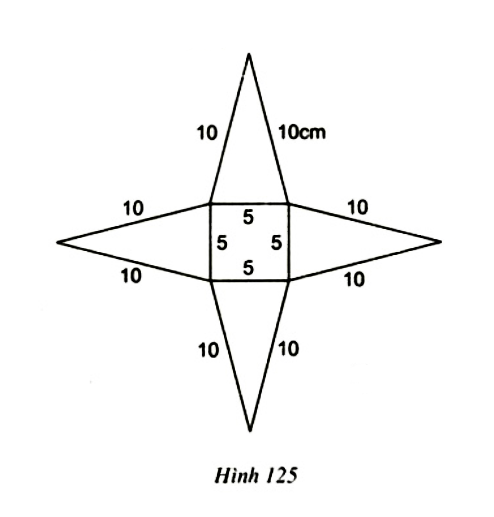
Bài 42 (SGK trang 121): Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước trên hình 125.

Bài 42 Trang 121 SGK Toán 8 tập 2

Hướng dẫn giải

- Định lý Pi – ta – go: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

- Chân đường cao của hình chóp đều là tâm của đường tròn đi qua các đỉnh của mặt đáy.

Lời giải chi tiết

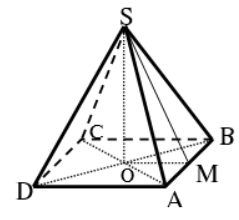
Bài 42 Trang 121 SGK Toán 8 tập 2

Gọi O là giao điểm hai đường chéo của mặt phẳng đáy.

Khi đó đường cao của hình chóp đều là SO.

Từ O kẻ OM vuông góc với AB. Do ABCD là hình vuông suy ra M là trung điểm của AB ⇒ MA = MB = MO = 2,5

Mặt khác SAB là tam giác cân suy ra SM ⊥ AB

Ta có tam giác MSB vuông tại M, áp dụng định lý Pi – ta – go ta có:

$S{B^2} = S{M^2} + M{B^2} \Rightarrow SM = \sqrt {S{B^2} - M{B^2}} = \sqrt {{{10}^2} - {{\left( {2,5} \right)}^2}} \approx 9,7cm$

Xét tam giác SOM vuông tại O, áp dụng định lý Pi – ta – go ta có:

$S{M^2} = S{O^2} + M{O^2} \Rightarrow SO = \sqrt {S{M^2} - M{O^2}} = \sqrt {9,{7^2} - 2,{5^2}} \approx 9,4cm$

_{------------------------------------------------------------}

Trên đây là lời giải chi tiết bài tập Toán 8 Diện tích xung quanh của hình chóp đều cho các em học sinh tham khảo, nắm được cách giải các dạng toán Chương 4: Hình lăng trụ đứng, Hình chóp đều Toán 8 Tập 2. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 8. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!