Giaitoan.com Toán 7 Giải Toán 7 Kết nối tri thức

Bài 4.23 trang 84 Toán 7 tập 1 SGK Kết nối tri thức với cuộc sống Giải Toán 7 Kết nối tri thức

Nội dung
  • 27 Đánh giá

Bài 4.23 trang 84 SGK Toán 7

Toán 7 Bài 4.23 trang 84 Tam giác cân. Đường trung trực của đoạn thẳng là lời giải bài SGK Toán 7 Tập 1 KNTT hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 4.23 Toán 7 trang 84

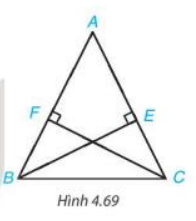
Bài 4.23 trang 84 Toán 7 tập 1: Cho tam giác ABC cân tại a và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.

Bài 4.23 trang 84 Toán 7 tập 1 SGK Kết nối tri thức với cuộc sống

Hướng dẫn giải

– Tam giác cân là tam giác có hai cạnh bằng nhau.

– Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

– Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

– Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Lời giải chi tiết

Ta có: Tam giác ABC cân tại A nên AB = AC và \widehat{ABC}=\widehat{ACB}

Cách 1: Xét tam giác AEB vuông tại E và tam giác AFC vuông tại F ta có:

Góc A chung

AB = AC (cmt)

Do đó ∆ AEB = ∆ AFC (cạnh huyền – góc nhọn)

Suy ra BE = CF (hai cạnh tương ứng)

Cách 2: Xét tam giác EBC vuông tại E và tam giác FCB vuông tại F ta có:

\widehat{ABC}=\widehat{ACB} (cmt)

Cạnh BC chung

Do đó ∆ EBC = ∆ FCB (cạnh huyền – góc nhọn)

Suy ra BE = CF (hai cạnh tương ứng)

→ Câu hỏi cùng bài:

→ Bài liên quan: Giải Toán 7 Chân trời sáng tạo Bài 16 Tam giác cân. Các đường trung trực của đoạn thẳng

→ Bài tiếp theo: Giải Toán 7 Chân trời sáng tạo Luyện tập chung trang 85

----------------------------------------

Chia sẻ bởi: Song Tử
Mời bạn đánh giá!
  • Lượt xem: 9.270
Tìm thêm: Toán 7 Giải Toán 7
1 Bình luận
Sắp xếp theo
Xóa Đăng nhập để Gửi
  • Thảo Nguyễn
    Thảo Nguyễn

    Có cách 2 ko ạ


    Thích Phản hồi 20:24 26/11

    Chủ đề liên quan

    Mới nhất trong tuần