Bài 13 trang 72 SGK Toán 9 tập 2

Giải SGK Toán 9

3 Đánh giá

Toán 9 Bài 2 Liên hệ giữa cung và dây

Giải Toán 9 bài 13 Trang 72 SGK Liên hệ giữa cung và dây với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 13 trang 72 SGK Toán 9 tập 2

Bài 13 (SGK trang 72): Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Hướng dẫn giải

+ Hai cung bằng nhau nếu chúng có số đo bằng nhau.

Lời giải chi tiết

TH1: Tâm đường tròn nằm ngoài hai dây song song

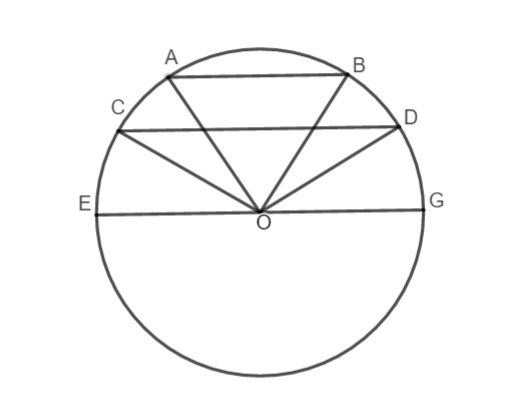
Bài 13 trang 72 SGK Toán 9 tập 2

Giả sử đường tròn (O) có hai dây song song AB // CD. Ta chứng minh cung AC bằng cung BD.

Qua O kẻ đường kính EG // CD $\Rightarrow E G / / A B$

Nối $OA,OC,OB,OD\Rightarrow OA=OB=OC=OD=R$ (bán kính)

+ Xét tam giác OAB cân tại O do OA = OB nên $\widehat{OAB}=\widehat{OBA}$ (1)

Lại có $E G / / A B \Rightarrow \widehat{O A B}=\widehat{A O E} ; \widehat{O B A}=\widehat{B O G}$ (so le trong) (2)

Từ (1) và (2) suy ra $\widehat{EOA}=\widehat{BOG}$ (*)

+ Xét tam giác OCD cân tại O do OC = OD nên $\widehat{OCD}=\widehat{ODC}$ (3)

Lại có $E G / / C D \Rightarrow \widehat{O C D}=\widehat{C O E} ; \widehat{O D C}=\widehat{D O G}$ (so le trong) (4)

Từ (3) và (4) suy ra $\widehat{E O C}=\widehat{D O G}\left({ }^{\star \star}\right)$

Từ (*) và (**) suy ra $\widehat{EOA}-\widehat{EOC}=\widehat{BOG}-\widehat{DOG}\Leftrightarrow \widehat{AOC}=\widehat{BOD}\Rightarrow \overset\frown{AC}=\overset\frown{BD}$

TH2: Tâm đường tròn nằm trong hai dây song song

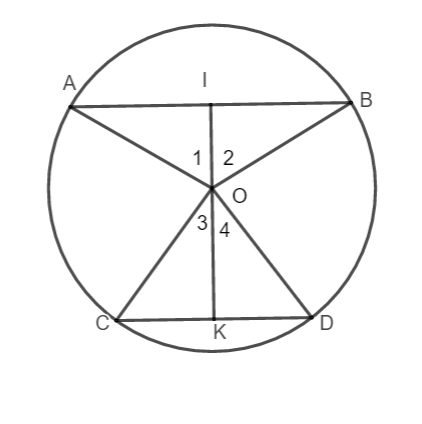
Bài 13 trang 72 SGK Toán 9 tập 2

Giả sử AB và CD là các dây song song của đường tròn (O). Ta chứng minh $\overset\frown{AC}=\overset\frown{BD}$

Kẻ $O I \perp A B(I \in A B)$ và $O K \perp C D(K \in C D)$

Do AB // CD nên I, O, K thẳng hàng.

Do các tam giác OAB, OCD là các tam giác cân đỉnh O nên các đường cao kẻ từ đỉnh đồng thời là phân giác.

Vì vậy ta có: $\widehat{O_{1}}=\widehat{O_{2}},\widehat{O_{3}}=\widehat{O_{4}}$

Ta có: $\widehat{A O C}=180^{0}-\widehat{O_{1}}-\widehat{O_{3}}=180^{0}-\widehat{O_{2}}-\widehat{O_{4}}=\widehat{B O D}$

Suy ra $\overset\frown{AC}=\overset\frown{BD}$

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán đại 9: Liên hệ giữa cung và dây. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!