Giaitoan.com Toán 9 Toán 9 Kết nối tri thức

Bài 1.5 Trang 10 Toán 9 Tập 1 Kết nối tri thức Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Nội dung
  • 5 Đánh giá

Bài 1.5 Trang 10 Toán 9 KNTT

Toán 9 Bài 1.5 Trang 10 là lời giải bài Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn SGK Toán 9 Kết nối tri thức hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 9. Mời các em học sinh cùng tham khảo chi tiết.

Giải Bài 1.5 Toán 9 Trang 10

Bài 1.5 trang 10 Toán 9 tập 1: Cho các cặp số (− 2; 1), (0; 2), (1; 0), (1,5; 3), (4; − 3) và hai phương trình

5x + 4y = 8, (1)

3x + 5y = − 3. (2)

Trong các cặp số đã cho:

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?

c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = − 3 trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.

Hướng dẫn:

Một cặp gồm hai phương trình bậc nhất hai ẩn ax + by = c và a'x + b'y = c' được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng:

\left\{ \begin{array}{l}ax+by=c\\a'x+b'y=c'\end{array} \right. (*)

Mỗi cặp số (x0; y0) được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lời giải chi tiết:

a) Với phương trình (1): 5x + 4y = 8

  • Thay x = − 2; y = 1, ta có:

5x + 4y = 5 . (− 2) + 4 . 1 = − 6 ≠ 8 nên (− 2; 1) không là nghiệm của phương trình (1).

  • Thay x = 0; y = 2, ta có:

5x + 4y = 5 . 0 + 4 . 2 = 8 nên (0; 2) là nghiệm của phương trình (1).

  • Thay x = 1; y = 0, ta có:

5x + 4y = 5 . 1 + 4 . 0 = 5 ≠ 8 nên (1; 0) không là nghiệm của phương trình (1).

  • Thay x = 1,5; y = 3, ta có:

5x + 4y = 5 . 1,5 + 4 . 3 = 19,5 ≠ 8 nên (1,5; 3) không là nghiệm của phương trình (1).

  • Thay x = 4; y = − 3, ta có:

5x + 4y = 5 . 4 + 4 . (− 3) = 8 nên (4; − 3) là nghiệm của phương trình (1).

Vậy cặp số là nghiệm của phương trình (1) là (0; 2) và (4; − 3).

b) Để các cặp số là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2) thì các cặp số đó phải là nghiệm chung của hai phương trình.

  • Thay x = 0; y = 2 vào phương trình (2), ta có:

3x + 5y = 3 . 0 + 5 . 2 = 10 ≠ − 3 nên (0; 2) không là nghiệm của phương trình (2).

  • Thay x = 4; y = - 3 vào phương trình (2), ta có:

3x + 5y = 3 . 4 + 5 . (− 3) = − 3 nên (4; − 3) là nghiệm của phương trình (2).

Vậy cặp số (4; − 3) là nghiệm chung của hai phương trình, nghĩa là (4; − 3) là nghiệm của hệ gồm phương trình (1) và phương trình (2).

c) Đường thẳng 5x + 4y = 8 đi qua hai điểm tùy ý là A(0; 2) và B(4; − 3).

Đường thẳng 3x + 5y = − 3 đi qua hai điểm tùy ý là B(4; − 3) và C(− 1; 0).

Ta có hình vẽ sau:

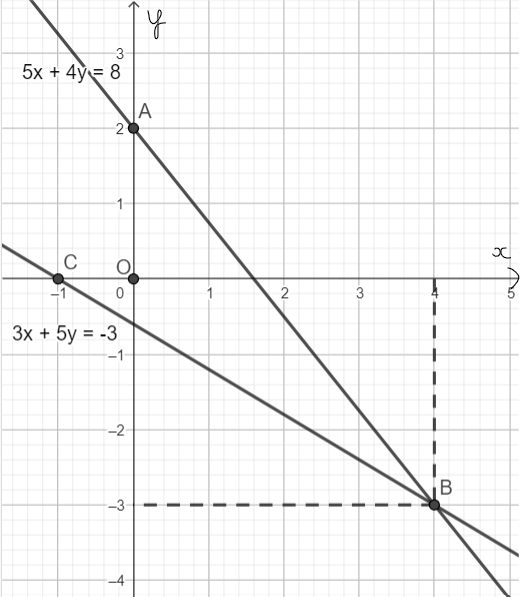
Vậy B(4; − 3) là giao điểm của hai đường thẳng 5x + 4y = 8 và 3x + 5y = – 3.

---> Câu hỏi cùng bài:

---> Bài liên quan: Toán 9 Kết nối tri thức Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

---> Bài tiếp theo: Toán 9 Kết nối tri thức Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn

--------------------------------------------

---> Tham khảo thêm: Đề thi giữa học kì 1 Toán 9 sách Kết nối tri thức

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 1.118
Tìm thêm: Toán 9 Toán 9 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần