Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Bài 1.16 trang 25 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 3

Nội dung
  • 1 Đánh giá

Bài 1.16 trang 25 Toán 12 KNTT

Toán 12 Bài 1.16 trang 25 Tập 1 là câu hỏi trong bài Bài 3: Đường tiệm cận của đồ thị hàm số với lời giải chi tiết giúp cho các em học sinh tham khảo, củng cố kỹ năng giải Toán 12 KNTT.

Giải Bài 1.16 Toán 12 trang 25

Bài 1.16 trang 25 toán 12 tập 1: Hình 1.26 là đồ thị của hàm số y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}

Sử dụng đồ thị này, hãy:

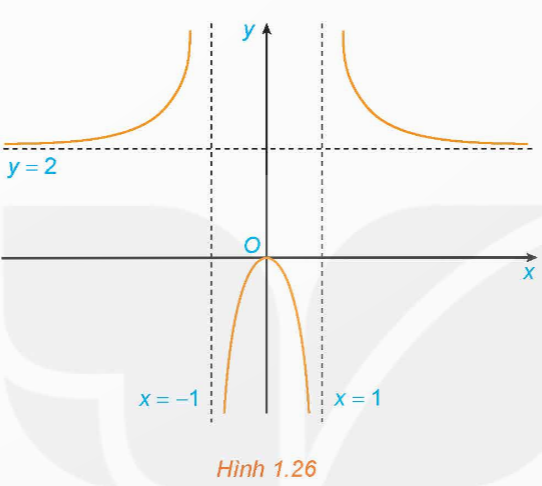
a) Viết kết quả của các giới hạn sau: \mathop {\lim }\limits_{x \to - \infty } f\left( x \right); \mathop {\lim }\limits_{x \to + \infty } f\left( x \right); \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right); \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)

b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Lời giải chi tiết:

a) Từ đồ thị ta có:

\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2

\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2

\mathop {\lim }\limits_{x \to 1^- } f\left( x \right) = -\infty

\mathop {\lim }\limits_{x \to - 1^+ } f\left( x \right) = -\infty

b) Đồ thị hàm số có:

Tiệm cận ngang: y = 2

Tiệm cận đứng: x = - 1 và x = 1.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 179
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần