Giaitoan.com Toán 12

Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến Tính đơn điệu của hàm số

Nội dung
  • 1 Đánh giá

Xét tính đơn điệu của hàm số

Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, GiaiToan.com xin mời quý thầy cô và các bạn học sinh tham khảo tài liệu Tìm tất cả các giá trị nguyên m để hàm số đồng biến nghịch biến. Bộ tài liệu giới thiệu đến bạn đọc các phương pháp giải bài tập ứng dụng tìm tham số m để hàm số có cực trị cùng hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.

Tìm m để hàm số đồng biến nghịch biến

Ví dụ 1: Có bao nhiêu giá trị nguyên của m ∈ [0; 2022] để hàm số y = {2021^{{x^3} - {x^2} - mx + 1}} nghịch biến trên [-1; 2].

A. 2021

B. 2015

C. 2020

D. 2014

Hướng dẫn giải

Hàm số y = {2021^{{x^3} - {x^2} - mx + 1}} nghịch biến trên [-1; 2]

\Leftrightarrow y' \leqslant 0\,\,\forall x \in \left[ { - 1\,;\,2} \right]

\Leftrightarrow 3{x^2} - 2x - m \leqslant 0\,\,\forall x \in \left[ { - 1;2} \right]

\Leftrightarrow 3{x^2} - 2x \leqslant m\,\,\forall x \in \left[ { - 1;2} \right]

Đặt f(x) = 3x2 – 2x; f’(x) = 6x - 2

Bảng biến thiên:

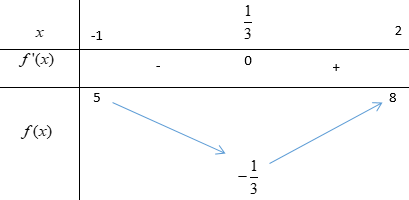
Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến

Từ bảng biến thiên suy ra f(x) ≤ 8, ∀ x ∈[-1; 2]

=> m ≥ 8

Vì m nguyên và nên có 2015 giá trị m thỏa mãn.

Đáp án B

Ví dụ 2: Số giá trị nguyên của tham số m thuộc đoạn [-2020; 2021] sao cho hàm số y = {\left( {\frac{1}{e}} \right)^{\frac{{x - 4}}{{x - 2m}}}} nghịch biến trên khoảng (0; 2) là

A. 2021

B. 2022

C. 2020

D. 2019

Hướng dẫn giải

Ta có: y = {\left( {\frac{1}{e}} \right)^{\frac{{x - 4}}{{x - 2m}}}} \Rightarrow y' = {\left( {\frac{{x - 4}}{{x - 2m}}} \right)^\prime }.{\left( {\frac{1}{e}} \right)^{\frac{{x - 4}}{{x - 2m}}}}.\ln \left( {\frac{1}{e}} \right)

Để hàm số nghịch biến trên khoảng (0; 2) thì y’ < 0, ∀ x ∈(0; 2)

\Leftrightarrow {\left( {\dfrac{{x - 4}}{{x - 2m}}} \right)^\prime }.\underbrace {{{\left( {\dfrac{1}{e}} \right)}^{\dfrac{{x - 4}}{{x - 2m}}}}}_{ > 0,\,\forall x \in \left( {0;2} \right)}.\underbrace {\ln \left( {\dfrac{1}{e}} \right)}_{ < 0} < 0,\,\forall x \in \left( {0;2} \right)

\Leftrightarrow {\left( {\frac{{x - 4}}{{x - 2m}}} \right)^\prime } > 0,\forall x \in \left( {0;2} \right)\,

\Leftrightarrow \frac{{ - 2m + 4}}{{{{\left( {x - 2m} \right)}^2}}} > 0,\,\forall x \in \left( {0;2} \right)\,

\Leftrightarrow \left\{ \begin{gathered} - 2m + 4 > 0 \hfill \\ x \ne 2m \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 2 \hfill \\ \left[ \begin{gathered} 2m \leqslant 0 \hfill \\ 2m \geqslant 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 2 \hfill \\ \left[ \begin{gathered} m \leqslant 0 \hfill \\ m \geqslant 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} 1 \leqslant m < 2 \hfill \\ m \leqslant 0 \hfill \\ \end{gathered} \right.

Mặt khác, m \in \left[ { - 2020;2021} \right] \Rightarrow m \in \left[ { - 2020;0} \right] \cup \left[ {1;2} \right)

Vì m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;0; - 1; - 2;...; - 2020} \right\}

=> Có 2022 giá trị nguyên của m

Đáp án B

Ví dụ 3: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để hàm số y = {{\text{e}}^{\frac{1}{3}\left( {{m^2} - 2m} \right){x^3} + m{x^2} + 3x}} đồng biến trên tập số thực?

A. 21

B. 19

C. 20

D. 18

Hướng dẫn giải

Ta có y' = \left[ {\left( {{m^2} - 2m} \right){x^2} + 2mx + 3} \right] \cdot {{\text{e}}^{\frac{1}{3}\left( {{m^2} - 2m} \right){x^3} + m{x^2} + 3x}}

Hàm số đồng biến trên R

\Leftrightarrow g\left( x \right) = \left( {{m^2} - 2m} \right){x^2} + 2mx + 3 \geqslant 0,\forall x \in \mathbb{R}

Nếu m = 0, ta có g(x) = 3 > 0 nên m = 0 (thỏa mãn)

Nếu m = 2, hàm số g(x) = 4x + 3

Bảng xét dấu

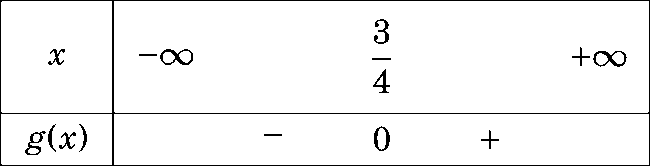
Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến

Suy ra g\left( x \right) \geqslant 0 \Leftrightarrow x \geqslant \frac{3}{4} nên m = 2 (không thỏa mãn)

Với \left\{ \begin{gathered} m \ne 0 \hfill \\ m \ne 2 \hfill \\ \end{gathered} \right.. Ta có

g\left( x \right) \geqslant 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{gathered} {m^2} - 2m > 0 \hfill \\ {m^2} - 3\left( {{m^2} - 2m} \right) \leqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} m < 0 \hfill \\ m > 2 \hfill \\ \end{gathered} \right. \hfill \\ \left[ \begin{gathered} m \leqslant 0 \hfill \\ m \geqslant 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m < 0 \hfill \\ m \geqslant 3 \hfill \\ \end{gathered} \right.

=> m \in \left\{ { - 10, - 9, \ldots - 1,0} \right\} \cup \left\{ {3,4,5, \ldots 9,10} \right\}

Vậy có giá trị m thỏa mãn yêu cầu bài toán.

Đáp án B

Ví dụ 4: Có bao nhiêu giá trị nguyên của tham số m để hàm số y = {{\text{2}}^{\frac{1}{3}{x^3} + \frac{m}{2}{x^2} - 6{m^2}x + 2022}} đồng biến trên khoảng (2; 3)?

A. 1

B. 2

C. Vô số

D. 0

Hướng dẫn giải

Ta có y' = \left( {{x^2} + mx - 6{m^2}} \right) \cdot {{\text{2}}^{\frac{1}{3}{x^3} + \frac{m}{2}{x^2} - 6{m^2}x + 2022}} \cdot \ln 2

Hàm số đồng biến trên R

\Leftrightarrow g\left( x \right) = {x^2} + mx - 6{m^2} \geqslant 0,\forall x \in \mathbb{R} \Leftrightarrow \Delta \leqslant 0 \Leftrightarrow 25{m^2} \leqslant 0 \Leftrightarrow m = 0

+ Phương trình g\left( x \right) = 0 \Leftrightarrow {x^2} + mx - 6{m^2} = 0 \Leftrightarrow \left[ \begin{gathered} x = 2m \hfill \\ x = - 3m. \hfill \\ \end{gathered} \right.

Ta xét các trường hợp:

TH1: 2m = -3m => m = 0. Khi đó g\left( x \right) = {x^2} \geqslant 0,\forall x \in \mathbb{R}

=> m = 0 (thỏa mãn)

TH2: 2m > -3m => m > 0.

Ta có bảng biến thiên

Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến

Từ bảng biến thiên, suy ra hàm số đồng biến trên (-∞; -3m) và (2m; +∞)

Hàm số đã cho đồng biến trên khoảng (2; 3) khi

\left[ \begin{gathered} \left( {2;3} \right) \subset \left( { - \infty ; - 3m} \right) \hfill \\ \left( {2;3} \right) \subset \left( {2m; + \infty } \right) \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} - 3m \geqslant 3 \hfill \\ 2m \leqslant 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m \leqslant - 1 \hfill \\ m \leqslant 1 \hfill \\ \end{gathered} \right. \Leftrightarrow m \leqslant 1.

Kết hợp cùng điều kiện: 0 < m ≤ 1

TH3: 2m < -3m => m < 0.

Ta có bảng biến thiên

Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến

Từ bảng biến thiên, suy ra hàm số đồng biến trên (-∞; 2m) và (-3m; +∞)

Hàm số đã cho đồng biến trên khoảng (2; 3) khi

\left[ \begin{gathered} \left( {2;3} \right) \subset \left( { - \infty ;2m} \right) \hfill \\ \left( {2;3} \right) \subset \left( { - 3m; + \infty } \right) \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} 2m \geqslant 3 \hfill \\ - 3m \leqslant 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m \geqslant \frac{3}{2} \hfill \\ m \geqslant - \frac{2}{3} \hfill \\ \end{gathered} \right. \Leftrightarrow m \geqslant - \frac{2}{3}.

So với điều kiện, ta nhận \frac{{ - 2}}{3} \leqslant m < 0

Vậy - \frac{2}{3} \leqslant m \leqslant 1 thỏa yêu cầu bài toán.

Do m \in \mathbb{Z} nên m = 0 hoặc m = 1

Đáp án B

Ví dụ 5: Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019; 2019) để hàm số y = x + m + \sqrt {{x^2} + 2(m + 1)x + {m^2} + 2m + 4} + {\log _2}\left( {x - m + \sqrt {2{x^2} + 1} } \right) có tập xác định là D = \mathbb{R}

A. 2020

B. 2021

C. 2018

D. 2019

Hướng dẫn giải

Hàm số xác định với mọi x \in \mathbb{R} thì \left\{ {\begin{array}{*{20}{l}} {{x^2} + 2(m + 1)x + {m^2} + 2m + 4 \geqslant 0} \\ {x - m + \sqrt {2{x^2} + 1} > 0} \end{array}} \right. luôn đúng với mọi x \in \mathbb{R}

Ta có:

{x^2} + 2(m + 1)x + {m^2} + 2m + 4 = \left[ {x + \left( {m + 1} \right)} \right]_{}^2 + 3 > 0,\forall x \in \mathbb{R}

Ta có:

x - m + \sqrt {2{x^2} + 1} > 0,\forall x \in \mathbb{R} \Leftrightarrow x + \sqrt {2{x^2} + 1} > m,\forall x \in \mathbb{R}

Xét hàm số f(x) = x + \sqrt {2{x^2} + 1} với x \in \mathbb{R} có

{f^\prime }(x) = 1 + \frac{{2x}}{{\sqrt {2{x^2} + 1} }};{f^\prime }(x) = 0 \Leftrightarrow x = \frac{{ - 1}}{{\sqrt 2 }}

Xét bảng biến thiên

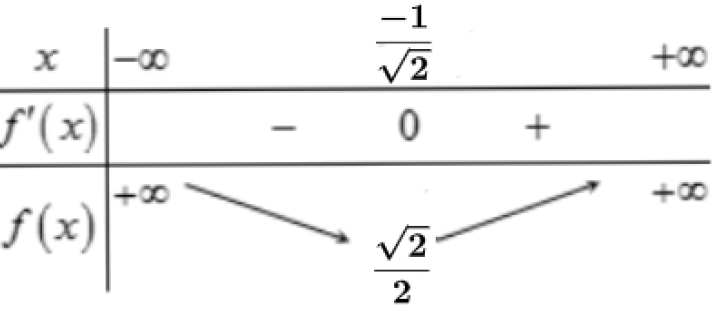
Tìm giá trị nguyên của m để hàm số đồng biến, nghịch biến

Từ bảng biến thiên ta thấy để x + \sqrt {2{x^2} + 1} > m,\forall x \in \mathbb{R} \Leftrightarrow \frac{{\sqrt 2 }}{2} > m

Kết hợp điều kiện \left\{ {\begin{array}{*{20}{l}} {m \in \mathbb{Z}} \\ {m \in ( - 2019;2019)} \end{array} \Rightarrow m \in \{ - 2018, - 2017, - 2016, \ldots , - 1,0\} } \right.

Kết luận: có 2019 giá trị của m thỏa mãn bài toán.

Đáp án D

---------------------------------------------------------------

Trên đây GiaiToan đã giới thiệu đến thầy cô và học sinh tài liệu Tìm tham số m để hàm số thỏa mãn điều kiện, hy vọng tài liệu sẽ là công cụ hữu ích giúp học sinh ôn thi THPT Quốc gia hiệu quả.

Chia sẻ bởi: Bọ Cạp
Mời bạn đánh giá!
  • Lượt xem: 1.460
Tìm thêm: Toán 12 Công thức Toán 12
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần