Giaitoan.com Toán 12

Số phức là gì? Công thức số phức

Nội dung
  • 2 Đánh giá

Số phức

Bài tập số phức đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về dạng toán biến đổi số phức lớp 12. Tài liệu bao gồm định nghĩa, công thức, cách biểu diễn và tính chất của số phức cùng với đó là các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề lượng giác. Chúc các bạn học tập hiệu quả!

A. Công thức số phức

Cho số phức z = a + bi \left( {a;b \in \mathbb{R}} \right). Khi đó:

a là phần thức, b là phần ảo

Nếu a = 0 thì z là số thuần ảo

I là đơn vị ảo với i2 = -1

Nếu b = 0 thì x là một số thực

Ví dụ: Số phức z = 1 + 2i, z = 8 – 3i; ….

z = 1 là một số thực

z = 2i là một số thuần ảo; …

B. Quan hệ giữa các tập hợp số

- Tập số phức kí hiệu là \mathbb{C}

- Quan hệ các tập hợp số \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}

C. Hai số phức bằng nhau

Cho z1 = a + bi và z2 = c + di với \left( {a;b;c;d \in \mathbb{R}} \right). Khi đó:

z1 = z2 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = c} \\ {b = d} \end{array}} \right.

z1 = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 0} \\ {b = 0} \end{array}} \right.

D. Biểu diễn hình học của số phức

Mỗi số phức z = a + bi được biểu diễn bởi duy nhất một điểm M(a; b) trên mặt phẳng tọa độ

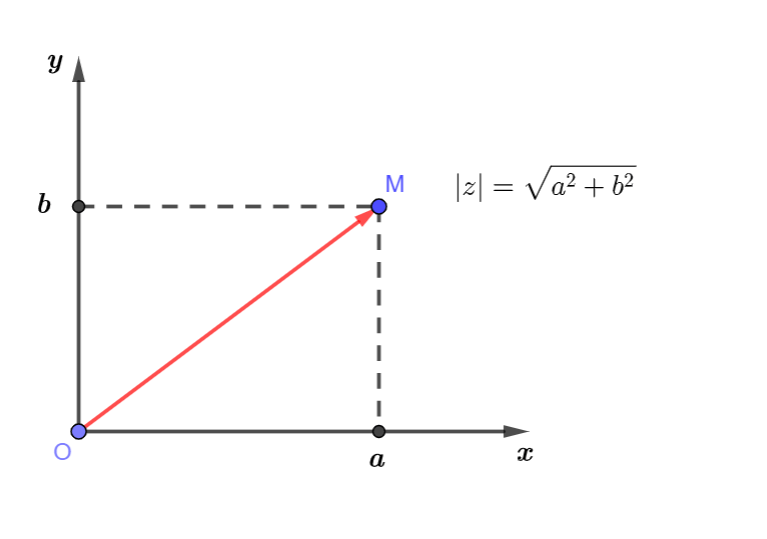
Số phức là gì

E. Mô đun số phức

Độ dài của véc tơ OM được gọi lag mô đun của số phức z và kí hiệu là |z|

- Từ định nghĩa, suy ra \left| z \right| = \sqrt {{a^2} + {b^2}} hay \left| {a + bi} \right| = \sqrt {{a^2} + {b^2}}

F. Số phức liên hợp

Số phức liên hợp của z kí hiệu là \overline z

Suy ra

\overline z = a - bi hay \overline {a + bi} = a - bi

Chú ý:

z.\overline z = {\left| z \right|^2} = {a^2} + {b^2}

Điểm biểu diễn z và \overline z đối xứng nhau qua Ox

G. Bài tập xác định số phức

Ví dụ: Xác định phần thực và phần ảo của số phức z, biết:

a) z = (3 – 2i) + (2 + i)

b) z = (3 – 2i)(2 – i)

Hướng dẫn giải

a) z = (3 – 2i) + (2 + i)

=> z = 3 – 2i + 2 + i

=> z = 3 + 2 - 2i + i

=> z = 5 – i

Phần thực của số phức là 5

Phần ảo của số phức là -i

b) z = (3 – 2i)(2 – i)

=> z = 6 – 3i – 4i + 2i2

=> z = 6 – 7i – 2

=> z = 4 – 7i

Phần thực của số phức là 4

Phần ảo của số phức là -7i

--------------------------------------------

Hi vọng Chuyên đề Số phức là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Chia sẻ bởi: Bọ Cạp
Mời bạn đánh giá!
  • Lượt xem: 06
Tìm thêm: Toán 12 Bài tập Toán 12
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần