Giaitoan.com Toán 10 Giải Toán 10 KNTT Tập 1

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit Giải Toán 10 sách kết nối tri thức

Nội dung
  • 1 Đánh giá

Bài 2.6 trang 30 Toán 10 tập 1

Giải SGK Toán 10: Bài 2.6 trang 30 Hệ bất phương trình bậc nhất hai ẩn được GiaiToan hướng dẫn giúp các học sinh luyện tập về dạng bài tính nhanh. Hi vọng tài liệu này giúp các em học sinh tự củng cố kiến thức, luyện tập và nâng cao cách giải bài tập Toán lớp 10. Mời các em cùng các thầy cô tham khảo.

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải chi tiết

a) Vì gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn nên 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1

Nếu mua x kilôgam thịt bò và y kilôgam thịt lợn thì chứa số đơn vị protein là: 800x + 600y (đơn vị)

Do số đơn vị protein cần ít nhất là 900 đơn vị nên ta có:

800x + 600y ≥ 900

=> 8x + 6y ≥ 9

Nếu mua x kilôgam thịt bò và y kilôgam thịt lợn thì chứa số đơn vị lipit là: 200x + 400y (đơn vị)

Do số đơn vị lipit cần ít nhất là 400 đơn vị nên ta có:

200x + 400y ≥ 400

=> x + 2y ≥ 2

Khi đó ta có hệ bất phương trình: \left\{ {\begin{array}{*{20}{c}} {0 \leqslant x \leqslant 1,6} \\ {0 \leqslant y \leqslant 1,1} \\ {8x + 6y \geqslant 9} \\ {x + 2y \geqslant 2} \end{array}} \right.

Miền nghiệm của hệ bất phương trình trên là tứ giác ABCD với tọa độ các đỉnh A(0;1), B(1,6;0,2) và C(1,6;1,1), D(0;1,1)

Hình vẽ minh họa:

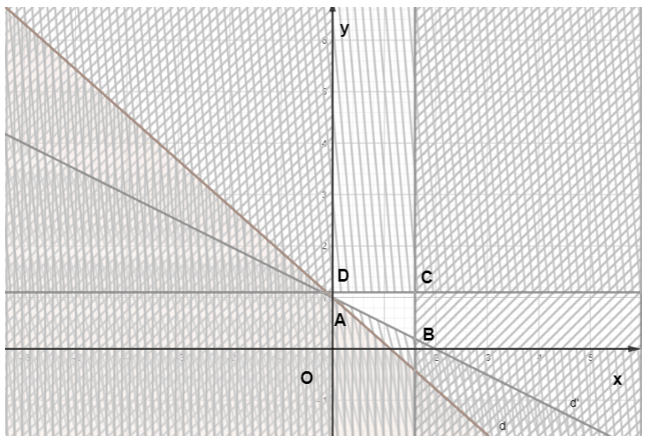
Bài 2.6 trang 30 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

b) Số tiền gia đình đó phải trả để mua x kilôgam thịt bò và y kilôgam thịt lợn là:

F(x;y) = 250x + 160y (nghìn đồng)

Vậy F(x;y) = 250x + 160y

c) Tính giá trị của biểu thức F tại các đỉnh của tam giác này:

F(1;0) = 250.1 + 160.0 = 250;

F(1,6;0,2) = 250.1,6 + 160.0,2 = 432;

F(1,6;1,1) = 250.1,6 + 160.1,1 = 576;

F(0;1,1) = 250.0 + 160.1,1 = 176;

Suy ra giá trị nhỏ nhất cần tìm là F(0;1,1) = 176.

Vậy để chi phí mua là ít nhất thì gia đình cần mua 0 kilôgam thịt bò và 1,1 kilôgam thịt lợn.

A. Hệ bất phương trình bậc nhất hai ẩn

- Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.

- Cặp số (x0; y0) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x0; y0) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.

B. Giải hệ bất phương trình bậc nhất hai ẩn

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

 Cách giải hệ bất phương trình bậc nhất hai ẩn.

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

----> Bài học liên quan: Toán 10 Bài 4 Hệ bất phương trình bậc nhất hai ẩn

-------------------------------------------------

Ngoài dạng bài tập Chuyên đề Toán 10: Giải hệ bất phương trình bậc nhất hai ẩn các em học sinh có thể tham khảo thêm nhiều nội dung Hỏi đáp Toán lớp 10 được GiaiToan đăng tải. Với phiếu bài tập này sẽ giúp các em rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các em học tập tốt!

Chia sẻ bởi: Su kem
Mời bạn đánh giá!
  • Lượt xem: 596
Tìm thêm: Toán 10 Giải Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần