Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Luyện tập 2 trang 29 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 4

Nội dung
  • 1 Đánh giá

Luyện tập 2 trang 29 Toán 12 KNTT

Toán 12 Luyện tập 2 trang 29 Tập 1 là câu hỏi trong bài Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số với lời giải chi tiết giúp cho các em học sinh tham khảo, củng cố kỹ năng giải Toán 12 Kết nối tri thức.

Giải Luyện tập 2 Toán 12 trang 29

Luyện tập 2 trang 29 toán 12 tập 1: Giải bài toán ở tình huống mở đầu, coi f(x) là hàm số xác định với x ≥ 1.

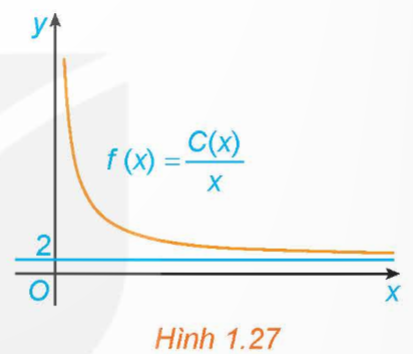
Bài toán: Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 45 (triệu đồng). Khi đó chi phí trung bình cho mỗi đơn vị sản phẩm là f(x) = \frac{C_{(x)} }{x}. Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào? 

Lời giải chi tiết:

Tập xác định của hàm số f(x) = \frac{C_{(x)} }{x} là: (0; + ∞).

Ta có: f'\left(x\right)=-\frac{45}{x^2}. Vậy f'(x) < 0 với mọi x ∈ [1; + ∞).

 \lim_{x\rightarrow + \infty} y =\lim_{x\rightarrow + \infty} \left (\frac{2x+45}{x} \right ) = 2

Do đó chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm

Trên hình 1.27, trong khoảng [1; +∞) đồ thị hàm số đi xuống và tiến gần đến TCN y= 2.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Kết nối tri thức Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 06
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

Chủ đề liên quan

Mới nhất trong tuần