Giaitoan.com Toán 12 Toán 12 Cánh diều

Hoạt động 1 trang 5 Toán 12 tập 1 Cánh diều Giải Toán 12 Cánh diều Chương 1 Bài 1

Nội dung
  • 1 Đánh giá

Hoạt động 1 trang 5 SGK Toán 12

Toán 12 Hoạt động 1 trang 5 tập 1 trong bài Bài 1 Tính đơn điệu của hàm số SGK Toán 12 Cánh diều được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Hoạt động 1 Toán 12 trang 5

Hoạt động 1 trang 5 toán 12 tập 1:

a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng.

b) Cho hàm số y = f(x) = x2 có đồ thị như Hình 2.

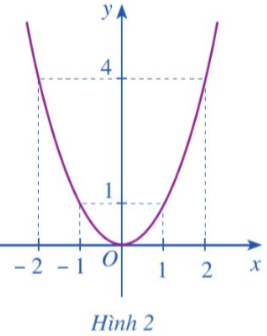
  • Xác định khoảng đồng biến, nghịch biến của hàm số đó.
  • Xét dấu của đạo hàm f'(x) = 2x.
  • Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số f(x) = x2 và dấu của đạo hàm f'(x) = 2x trên mỗi khoảng (– ∞; 0), (0; + ∞).
  • Hoàn thành bảng biến thiên sau.

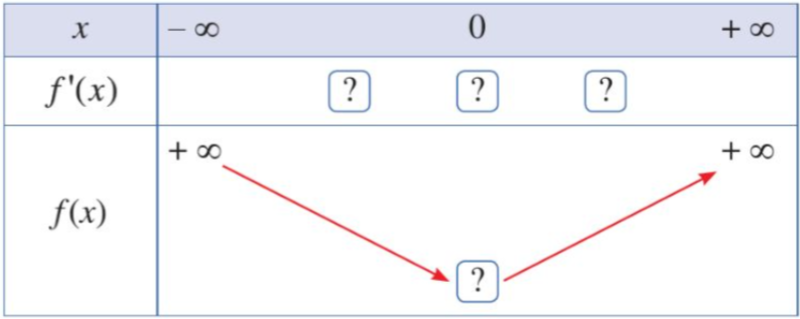
Lời giải chi tiết:

a) Cho hàm số y = f(x) xác định trên K.

+ Hàm số y = f(x) gọi là đồng biến trên K nếu ∀ x1, x2 thuộc K, x1 < x2 ⇒ f(x1) < f(x2).

+ Hàm số y = f(x) gọi là nghịch biến trên K nếu ∀ x1, x2 thuộc K, x1 < x2 ⇒ f(x1) > f(x2).

b) Từ đồ thị:

  • Hàm số y = f(x) nghịch biến trên khoảng (– ∞; 0); đồng biến trên khoảng (0; + ∞).
  • Ta có f'(x) = 2x > 0 với mọi x ∈ (0; + ∞) và f'(x) = 2x < 0 với mọi x ∈ (– ∞; 0).
  • Mối liên hệ:

+ Ta có f'(x) < 0, hàm số f(x) nghịch biến trên khoảng (– ∞; 0)

+ Ta có f'(x) > 0, hàm số f(x) đồng biến trên khoảng (0; + ∞)

  • Bảng biến thiên:

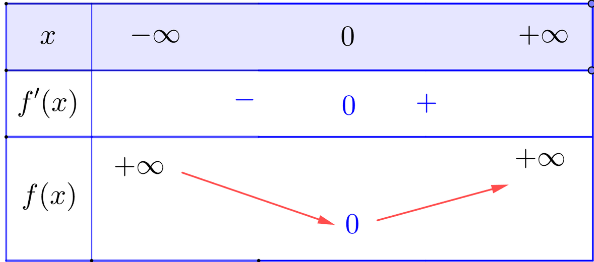
---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Cánh diều Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 14
Tìm thêm: Toán 12 Toán 12 Cánh diều
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần