Bài 6 trang 14 Toán 12 tập 1 Cánh diều Giải Toán 12 Cánh diều Chương 1 Bài 1

Bài 6 trang 14 SGK Toán 12

Toán 12 Bài 6 trang 14 tập 1 trong bài Bài 1 Tính đơn điệu của hàm số SGK Toán 12 Cánh diều được giải chi tiết giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải toán. Mời các em học sinh tham khảo.

Giải Bài 6 Toán 12 trang 14

Lời giải chi tiết:

Xét hàm số y = V(T) = 999,87 – 0,06426T + 0,0085043T² – 0,0000679T³

Ta có: y' = - 0,0002037T² + 0,0170086T - 0,06426

y' = 0 ⇔ T = 3,966 (vì 0 ≤ T ≤ 30)

Bảng biến thiên của hàm số y = V(T):

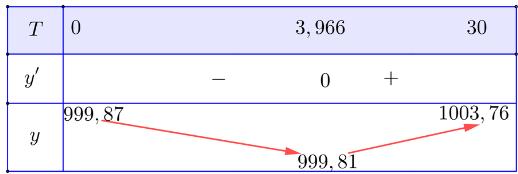
Vậy thể tích V(T), 0 ≤ T ≤ 30, giảm trong khoảng (0; 3,996)

---> Câu hỏi cùng bài:

• Bài 3 trang 13 toán 12 tập 1: Tìm các khoảng đơn điệu của mỗi hàm số sau:
• Bài 4 trang 13 toán 12 tập 1: Tìm điểm cực trị của mỗi hàm số sau:
• Bài 5 trang 14 toán 12 tập 1: Cho hai hàm số y = f(x) = x⁴ - 2x² + 2
• Bài 7 trang 14 toán 12 tập 1: Kính viễn vọng không gian Hubble được đưa vào vũ trụ

-------> Bài tiếp theo: Giải Toán 12 Cánh diều Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số