Đề thi giữa kì 1 môn Toán lớp 8 năm học 2022 - 2023 - Đề số 5 Đề kiểm tra giữa kì 1 môn Toán lớp 8

1 Đánh giá

Đề thi giữa kì 1 toán 8 năm học 2022-2023 - Đề 5

Đề thi giữa kì 1 lớp 8 môn Toán năm học 2022-2023- Đề 5

Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 5 được Giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì môn Toán 8. Mời các bạn cùng tham khảo chi tiết!

Đề thi giữa kì 1 lớp 8 môn Toán

A. Đề thi Toán giữa kì 1 lớp 8

Bản quyền thuộc về GiaiToan
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

I. TRẮC NGHIỆM

Câu 1: Khai triển hằng đẳng thức ta được kết quả

A. ${\left( {x - 2y} \right)^3}$

B. ${x^3} - 2{y^3}$

C. ${x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}$

$\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right)$

Câu 2: Kết quả của phép tính $- {x^2}\left( {3 - 2x} \right)$ là

A. $3{x^2} - 2{x^3}$

B. $2{x^3} - 3{x^2}$

C. $- 3{x^2} + 2{x^3}$

D. $- 4{x^2}$

Câu 3: Để thành một hẳng đẳng thức thì giá trị của $4{y^2} - 8y + ....$ …là

A. 4

B.9

C.16

D.25

Câu 4: Giá trị của biểu thức ${1001^2} - 1$ là

A. ${1000^2}$

B. $1002000$

C. 1000

D. 100200

Câu 5: Tìm x biết $4{x^2} - 9 = 0$ . Giá trị của x là

A. $\frac{2}{3};\frac{{ - 2}}{3}$

B. $\frac{3}{2};\frac{{ - 2}}{3}$

C. $\frac{3}{2};\frac{{ - 3}}{2}$

D. $\frac{2}{3};\frac{{ - 3}}{2}$

B. Phần tự luận

Câu 1: Phân tích đa thức thành nhân tử

$a)\,\,\,36{a^4} - {x^2}$

$b)\,\,\,{x^2} - 2x + 1 - {y^2}$

Câu 2: Tìm x biết

$a)\,\,\,x\left( {x - 4} \right) + 1 = 3x - 5$

$b)\,\,\,2{x^3} - {x^2} - 2x + 1 = 0$

Câu 3: Cho hình bình hành ABCD có AB > BC. Đường phân giác góc D cắt AB tại P, đường phân giác góc B cắt CD tại Q.

a) Chứng minh rằng AP = CQ

b) Chứng minh tứ giác DPBQ là hình bình hành.

c) Gọi H, K lần lượt là hình chiếu của P và Q trên BQ và DP. Chứng minh rằng hai đoạn thẳng AC và PQ cắt nhau tại trung điểm của mỗi đường.

Câu 4: Tìm giá trị nhỏ nhất của biểu thức: $A = - 2{x^2} - 10{z^2} + 4xz + 4x + 4z + 2016$

B. Đáp án đề thi Toán giữa kỳ 1 lớp 8

1. Phần trắc nghiệm

1. D

2.C

3. A

4.B

5.C

$a)\,\,\,36{a^4} - {x^2} = {\left( {6{a^2}} \right)^2} - {x^2} = \left( {6{a^2} - x} \right)\left( {6{a^2} + x} \right)$

2. Phần tự luận

Câu 1

$a)\,\,\,36{a^4} - {x^2} = {\left( {6{a^2}} \right)^2} - {x^2} = \left( {6{a^2} - x} \right)\left( {6{a^2} + x} \right)$

$b)\,\,\,{x^2} - 2x + 1 - {y^2} = {\left( {x - 1} \right)^2} - {y^2} = \left( {x - 1 - y} \right)\left( {x - 1 + y} \right)$

Câu 2

$\begin{array}{l} a)\,\,\,x\left( {x - 4} \right) + 1 = 3x - 5 \Leftrightarrow {x^2} - 4x + 1 - 3x + 5 = 0\\ \Leftrightarrow {x^2} - 7x + 6 = 0\\ \Leftrightarrow {x^2} - 6x - x + 6 = 0\\ \Leftrightarrow x\left( {x - 6} \right) - \left( {x - 6} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x - 1 = 0}\\ {x - 6 = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {x = 6} \end{array}} \right. \end{array}$

Vậy phương trình có nghiệm $x = 1$ hoặc $x = 6$

$\begin{array}{l} b)\,\,\,2{x^3} - {x^2} - 2x + 1 = 0\\ \Leftrightarrow \left( {2{x^3} - {x^2}} \right) - \left( {2x - 1} \right) = 0\\ \Leftrightarrow {x^2}\left( {2x - 1} \right) - \left( {2x - 1} \right) = 0\\ \Leftrightarrow \left( {2x - 1} \right)\left( {{x^2} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = \frac{1}{2}\\ x = 1\\ x = - 1 \end{array} \right. \end{array}$

Vậy phương trình có nghiệm $x = \frac{1}{2}$ hoặc $x = 1$ , hoặc $x = - 1$

Câu 3

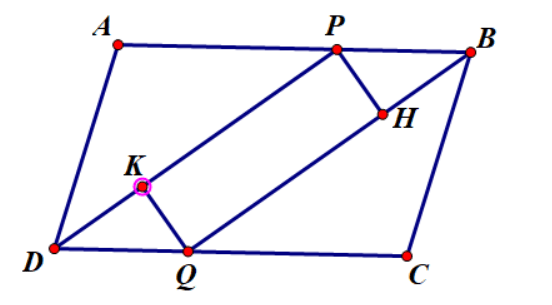
a) Xét tam giác ADP và tam giác QBC có:

$\left\{ \begin{array}{l} AD = BC\\ \widehat {ADP} = \widehat {CBQ} = \frac{1}{2}\widehat {ADC}\\ \widehat {DAB} = \widehat {BCD} \end{array} \right.$

b) Ta có $\left\{ \begin{array}{l} AB = AP + PB\\ DC = QC + DQ \end{array} \right.$ mà $\left\{ \begin{array}{l} AB = DC\\ AP = QC \end{array} \right. \Rightarrow PB = DQ$

Lại có $AB//CD \Rightarrow PB//DQ$ nên PBDQ là hình bình hành

c) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD O là trung điểm của DB, O là trung điểm của AC

Gọi O’ là giao điểm của hai đường chéo của hình bình hành PBDQ O’ là trung điểm của DB, O là trung điểm của PQ

Nên O là giao điểm của AC và PQ và cắt nhau tại trung điểm O của mỗi đường

Câu 4

$\begin{array}{l} A = - 2{x^2} - 10{z^2} + 4xz + 4x + 4z + 2016\\ = - 2\left[ {{x^2} - 2x\left( {y + 1} \right) + {{\left( {y + 1} \right)}^2} + \left( {4{y^2} - 4y + 1} \right) - 1010} \right]\\ = - 2{\left( {x - y - 1} \right)^2} - 2{\left( {2y - 1} \right)^2} + 2020 \end{array}$