Giaitoan.com Toán 7 Giải Toán 7 tập 2 KNTT

Câu hỏi 2 trang 82 SGK Toán 7 tập 2 Giải SGK Toán 7

Nội dung
  • 2 Đánh giá

Câu hỏi 2 trang 82 SGK Toán 7

Câu hỏi 2 trang 82 SGK Toán 7 tập 2 Tính chất ba đường cao của tam giác với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7. Tài liệu được biên soạn và đăng tải với hướng dẫn chi tiết các bài tập tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Chúc các bạn học tập tốt!

Giải câu hỏi 2 Toán 7 trang 82

Câu hỏi 2 (SGK trang 82): Hãy phát biểu và chứng minh các trường hợp còn lại của nhận xét trên (xem như những bài tập)

Nhận xét: Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh cà đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó là một tam giác cân.

Hướng dẫn giải

- Ba đường cao của một tam giác cùng đi qua một điểm.

- Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện của cạnh đó.

- Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đề ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.

Lời giải chi tiết

Bài tập 1: Nếu một tam giác có một đường trung trực đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

Hướng dẫn chứng minh

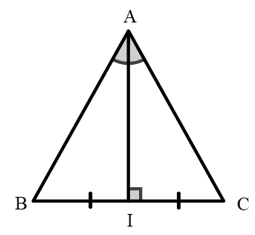
Câu hỏi 2 trang 82 SGK Toán 7 tập 2

Xét ΔABC có AI vừa là đường trung trực vừa là đường phân giác

AI là đường trung trực

=> AI ⊥ BC và I là trung điểm BC

Xét hai tam giác vuông ΔABI và ΔACI có:

\widehat {BAI} = \widehat {CAI} (AI là tia phân giác của \widehat {BAC})

Cạnh AI chung

=> ΔABI = ΔACI (góc nhọn – cạnh góc vuông)

=> AB = AC (hai cạnh tương ứng)

Vậy ΔABC cân tại A.

Bài tập 2: Nếu một tam giác có một đường trung trực đồng thời là đường cao thì tam giác đó là một tam giác cân.

Hướng dẫn chứng minh

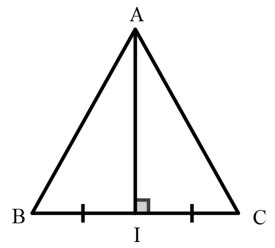
Câu hỏi 2 trang 82 SGK Toán 7 tập 2

Xét ΔABC có AI vừa là đường trung trực vừa là đường cao.

=> AI ⊥ BC và I là trung điểm BC.

Xét ΔABI và ΔACI ta có:

\widehat {AIB} = \widehat {AIC} = {90^0}

IB = IC (AI là đường trung trực)

AI là cạnh chung

=> ΔABI = ΔACI (hai cạnh góc vuông)

=> AB = AC (hai cạnh tương ứng)

Xét tam giác ABC có:

AB = AC

=> Tam giác ABC là tam giác cân tại A

Bài tập 3: Nếu một tam giác có một đường phân giác đồng thời là đường cao thì tam giác đó là một tam giác cân

Hướng dẫn chứng minh

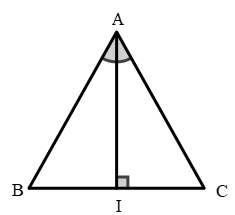
Câu hỏi 2 trang 82 SGK Toán 7 tập 2

Xét ΔABC có AI vừa là đường phân giác vừa là đường cao.

Vì AI là đường cao => AI ⊥ BC

Xét ΔABI và ΔACI ta có:

\widehat {AIB} = \widehat {AIC} = {90^0}

AI là cạnh chung

\widehat {BAI} = \widehat {CAI} (AI là phân giác của \widehat {BAC})

=> ΔABI = ΔACI (g – c - g)

=> AB = AC (hai cạnh tương ứng)

Xét tam giác ABC có:

AB = AC

=> Tam giác ABC là tam giác cân tại A.

Bài tập 4: Nếu một tam giác có một đường cao đồng thời là đường trung tuyến thì tam giác đó là một tam giác cân.

Hướng dẫn chứng minh

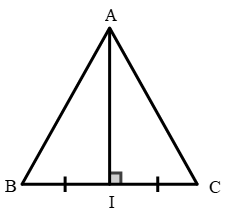
Câu hỏi 2 trang 82 SGK Toán 7 tập 2

Xét ΔABC có AI vừa là đường cao vừa là đường trung tuyến.

Ta sẽ đi chứng minh ΔABC cân tại A

Vì AI là đường cao => AI ⊥ BC

Vì AI là đường trung tuyến =>BI = CI

Xét ΔABI và ΔACI có:

AI là cạnh chung

\widehat {AIB} = \widehat {AIC} = {90^0}

BI = CI (AI là đường trung tuyến)

=> ΔABI = ΔACI (c – g - c)

=> AB = AC (hai cạnh tương ứng)

Xét tam giác ABC có:

AB = AC

=> Tam giác ABC cân tại A.

-----> Câu hỏi tiếp theo: Bài 58 trang 83 SGK Toán 7

-----------------------------------------------------

Trên đây là lời giải chi tiết Câu hỏi 2 trang 82 SGK Toán 7 tập 2 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 3 Quan hệ giữa các yếu tố trong tam giác, các đường đồng quy của tam giác. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 7. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!

Chia sẻ bởi: Sư Tử
Mời bạn đánh giá!
  • Lượt xem: 214
Tìm thêm: Toán 7 Giải Toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần