Bộ đề thi giữa kì 2 Toán 8 năm học 2020 - 2021 Đề kiểm tra giữa kì 2 Toán 8 có đáp án
Bộ đề thi giữa học kì 2 môn Toán lớp 8 mới nhất
- Đề kiểm tra giữa học kì 2 môn Toán lớp 8 năm học 2020 – 2021 Đề số 1
- Đề kiểm tra giữa học kì 2 môn Toán lớp 8 năm học 2020 – 2021 Đề số 2
- Đề kiểm tra giữa học kì 2 môn Toán lớp 8 năm học 2020 – 2021 Đề số 3
- Đề kiểm tra giữa học kì 2 môn Toán lớp 8 năm học 2020 – 2021 Đề số 4
- Đề kiểm tra giữa học kì 2 môn Toán lớp 8 năm học 2020 – 2021 Đề số 5
Việc ôn thi giữa học kì 2 của các bạn học sinh sẽ được trở nên thuận tiện hơn bao giờ hết khi sở hữu tài liệu: Bộ đề thi giữa học kì 2 môn Toán lớp 8. Tài liệu gồm nhiều đề thi giữa học kì 2 lớp 8 môn Toán có hướng dẫn đáp án chi tiết sẽ giúp các bạn học sinh làm quen với cấu trúc đề thi, rèn luyện các dạng bài tập có thể xuất hiện trong đề. Mời các bạn tham khảo.
Đề kiểm tra giữa kì 2 Toán 8 năm học 2020 – 2021 Đề số 1
Tham khảo: Đề thi giữa học kì 2 môn Toán lớp 8 Đề số 1
Đề kiểm tra giữa kì 2 Toán 8 năm học 2020 – 2021 Đề số 2
Tham khảo: Đề thi giữa học kì 2 môn Toán lớp 8 Đề số 2
Đề kiểm tra giữa kì 2 Toán 8 năm học 2020 – 2021 Đề số 3
Tham khảo: Đề thi giữa học kì 2 môn Toán lớp 8 Đề số 3
Đề kiểm tra giữa kì 2 Toán 8 năm học 2020 – 2021 Đề số 4
Tham khảo: Đề thi giữa học kì 2 môn Toán lớp 8 Đề số 4
Đề kiểm tra giữa kì 2 Toán 8 năm học 2020 – 2021 Đề số 5
Tham khảo: Đề thi giữa học kì 2 môn Toán lớp 8 Đề số 5
--------------------------------
Đề thi Toán 8 giữa học kì 2 - Đề số 1
Bài 1 (3 điểm): Giải phương trình:
| a. | b. |
| c. | d. |
Bài 2 (3 điểm): Giải bài toán bằng cách lập phương trình
Một người đi từ A đến B với vận tốc 30km/h. Một lúc sau người đó đi từ B về A với vận tốc lớn hơn vận tốc ban đầu 5km/h, vậy thời gian đi từ B về A ít hơn 30 phút so với lúc đi. Tính quãng đường AB.
Bài 3 ( 3.5 điểm): Cho tam giác ABC, trung tuyến AM, tia phân giác của góc AMB cắt AB tại D, tia phân giác của góc AMC cắt AC tại E.
a. Chứng minh: DE // BC
b. Cho cạnh BC = 6cm; AM = 5cm. Tính độ dài cạnh DE?
Bài 4 (0.5 điểm): Giải phương trình:
![]()
Đáp án đề thi Toán 8 giữa học kì 2 - Đề số 1
Bài 1:
a.

Vậy phương trình có nghiệm x = 3 hoặc ![]()
b.

Vậy phương trình có nghiệm x = 2 hoặc ![]()
c.

Vậy phương trình có nghiệm ![]()
d. ![]()
ĐKXĐ: 

Vậy phương trình có nghiệm ![]()
Bài 2:
Gọi quãng đường ban AB là x (km) x > 0
Thời gian đi từ A đến B là: ![]() (giờ)
(giờ)
Thời gian đi từ B đến A là: ![]() (giờ)
(giờ)
Do thời gian đi từ B về A ít hơn thời gian đi từ A đến B 30 phút = 0,5 giờ ta có phương trình:

Vậy quãng đường AB dài 105km.
Bài 3:
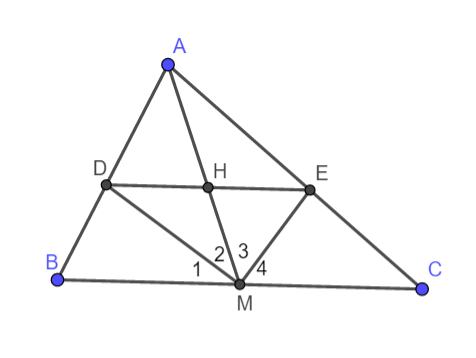
Xét tam giác ABM có:
![]() (Tính chất đường phân giác trong tam giác)(1)
(Tính chất đường phân giác trong tam giác)(1)
Xét tam giác AMC có:
![]() (Tính chất đường phân giác trong tam giác)(2)
(Tính chất đường phân giác trong tam giác)(2)
Từ (1) và (2) suy ra: ![]()
Theo định lý Talet ta suy ra DE // BC
b. Ta có BC = 6cm suy ra BM = MC = 3cm
Ta lại có:

Theo định lý Ta let cho tam giác ABC có:
![]()
Bài 4:

Vậy phương trình có nghiệm x = -2013
Đề thi Toán 8 giữa học kì 2 - Đề số 2
I. Phần trắc nghiệm (2 điểm)
Khoanh vào chữ cái trước câu trả lời đúng với từng câu hỏi.
Câu 1: Số nghiệm của phương trình (x2 - 4)(x - 1)(x + 2) = 0 là:
| A. 2 | B. 3 |
| C. 0 | D. 1 |
Câu 2: Trên hình vẽ, biết DE // BC, suy ra:
| A. | B. | 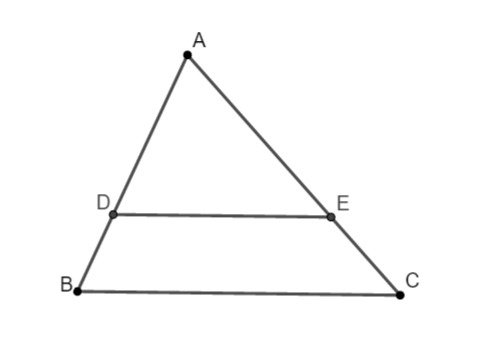 |
| C. | D. |
Câu 3: Nghiệm của phương trình 27 - 8x = 4x + 3 là:
| A. x = 2 | B. x = -2 |
| C. x = 1 | D. x = -1 |
Câu 4: Tìm x biết 14 - 3x ≥ 5 thì x có giá trị là:
| A. x > 3 | B. x < 3 |
| C. x ≤ 3 | D. x ≥ 3 |
II. Tự luận (8 điểm)
Bài 1 Giải phương trình:
| a) x(x - 3) + 2(x - 3) = 0 | b) |
Bài 2:
1. Giải bài toán bằng cách lập phương trình: Hai ô tô khởi hành cùng một lúc đi từ A đến B cách nhau 300km. Ô tô thứ nhất mỗi giờ chạy nhanh hơn ô tô thứ 2 là 10km nên đến B sớm hơn ô tô thứ hai 1 giờ. Tính vận tốc mỗi xe ô tô.
2. Tìm giá trị của m sao cho phương trình: (2x + 1)(2m + 8x) = 40 + 5(x + 3) có nghiệm x = 3
Bài 3: Cho tam giác nhọn ABC, có AB = 12cm, AC = 15 cm. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 4 cm, AE = 5cm
a, Chứng minh rằng: DE // BC, từ đó suy ra: ADE đồng dạng với ABC?
b, Từ E kẻ EF // AB (F thuộc BC). Tứ giác BDEF là hình gì? Từ đó suy ra: CEF đồng dạng EAD?
c, Tính độ dài các đoạn thẳng CF và FB khi biết độ dài cạnh BC = 18 cm?
Đáp án đề thi Toán 8 giữa học kì 2 - Đề số 2
I. Đáp án phần trắc nghiệm
| 1.B | 2.D | 3.A | 4.C |
II. Đáp án phần tự luận
Bài 1:
a) x(x - 3) + 2(x - 3) = 0
<=> (x + 2)(x - 3) = 0
<=> x + 2 = 0 hoặc x - 3 = 0
<=> x = -2 hoặc x = 3
Vậy x = 3 hoặc x = -2
b) Điều kiện xác định: x ≠ ∓5
x = -3
Bài 2:
1) Vận tốc xe thứ nhất là 60km/h, vận tốc xe thứ hai là 50km/h.
2) m = -7
Bài 3:
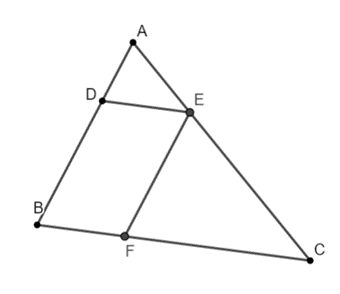 a) Theo định lí Talet ta có:
a) Theo định lí Talet ta có: ![]() => DE // BC. HS tự suy ra tam giác đồng dạng.
=> DE // BC. HS tự suy ra tam giác đồng dạng.
b) BDEF là hình bình hành. HS tự suy ra tam giác đồng dạng
c) CF = 12cm
(Còn tiếp)
----------------------------------------------------
Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Bộ đề thi giữa kì 2 toán 8 có đáp án năm học 2020 - 2021. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu liên quan: Giải Toán 8 Tập 1, Luyện tập Toán 8, Đề thi học kì 1 lớp 8, Đề thi giữa học kì 2 lớp 8, ....
Xem thêm bài viết khác

Đề ôn tập hè Toán lớp 7 lên lớp 8 năm 2022 Đề 4

Đề ôn tập hè Toán lớp 7 lên lớp 8 năm 2022 Đề 2

Các bước giải bài toán bằng cách lập phương trình































