Giaitoan.com Toán 7 Giải Toán 7 tập 2 KNTT

Bài 9.35 trang 83 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống Giải Toán 7 sách Kết nối tri thức

Nội dung
  • 2 Đánh giá

Bài 9.35 trang 83 SGK Toán 7 tập 2

GiaiToan mời các bạn tham khảo Bài 9.35 trang 83 Toán 7 tập 2 SGK KNTT thuộc bài Luyện tập chung trang 83 hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7.

Giải bài 9.35 Toán 7 trang 83

Bài 9.35 (SGK trang 83):

Kí hiệu SABC là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.

a) Chứng minh {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}

Gợi ý: Sử dụng GM = \dfrac{1}{3}AM để chứng minh {S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}.

b) Chứng minh {S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}.

Hướng dẫn:

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đồng quy của ba đường cao gọi là trọng tâm của tam giác đó.

Lời giải chi tiết

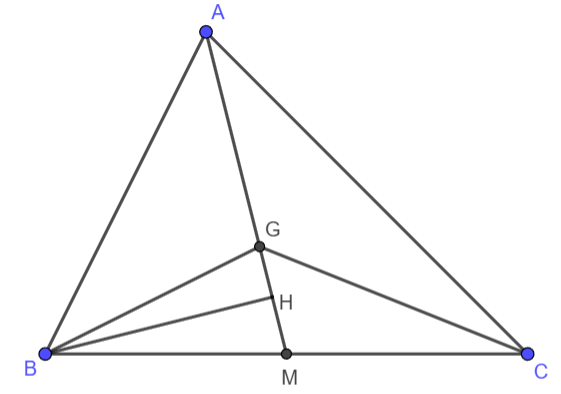
a) Do G là trọng tâm tam giác ABC nên GM = \dfrac{1}{3}AM

Kẻ BH ⊥ GM ta có

\begin{array}{l}{S_{GMH}} = \dfrac{1}{2}BH.GM\\{S_{ABM}} = \dfrac{1}{2}BH.AM\end{array}

\Rightarrow \dfrac{{{S_{GMH}}}}{{{S_{ABM}}}} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \Rightarrow {S_{GMH}} = \dfrac{1}{3}{S_{ABM}} (1)

Tương tự, ta có {S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)

Cộng 2 vế của (1) và (2) ta có:

\begin{array}{l}{S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \Rightarrow {S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\end{array}

→ Câu hỏi cùng bài:

→ Bài liên quan: Giải Toán 7 Kết nối tri thức Luyện tập chung trang 82

→ Bài tiếp theo: Giải Toán 7 Kết nối tri thức Bài 36: Hình hộp chữ nhật và hình lập phương

----------------------------------------

----------------------------------------

Chia sẻ bởi: nguyen hoang thu cuc
Mời bạn đánh giá!
  • Lượt xem: 2.832
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần