Bài 70 trang 141 SGK Toán 7 tập 1

Giải SGK Toán 7

1 Đánh giá

Giải Toán 7 Ôn tập chương 2: Tam giác

Bài 70 trang 141 SGK Toán 7 tập 1 với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 7. Tài liệu được biên soạn và đăng tải với hướng dẫn chi tiết các bài tập tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Chúc các bạn học tập tốt!

Bài 70 Trang 141 SGK Toán 7 - Tập 1

Bài 70 (SGK trang 141): Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a. Chứng minh rằng tam giác ANM là tam giác cân.

b. Kẻ $BH\bot AM\left( H\in AM \right)$ , kẻ $CK\bot AN\left( K\in AN \right)$ . Chứng minh rằng BH = CK.

c. Chứng minh rằng AH = AK.

d. Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?

e. Khi $\widehat{BAC}={{60}^{0}}$ và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC.

Hướng dẫn giải

- Tam giác cân là tam giác có hai cạnh bên và hai góc ở đáy bằng nhau.

- Chứng minh hai cạnh bằng nhau ta chứng minh hai tam giác bằng nhau.

- Chứng minh một tam giác là tam giác đều ta chứng minh tam giác cân có một góc bằng ${{60}^{0}}$

Lời giải chi tiết

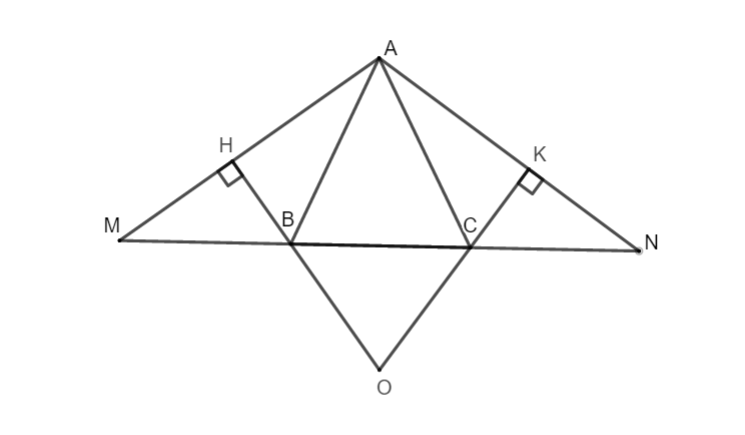
Bài 70 trang 141 SGK Toán 7 tập 1

a. Ta có: $\left\{ \begin{matrix} \widehat{ABM}+\widehat{ABC}={{180}^{0}} \\ \widehat{ACB}+\widehat{ACN}={{180}^{0}} \\ \end{matrix} \right.$

Mặt khác $\widehat{ABC}=\widehat{ACB}$ (do tam giác ABC cân tại A)

$\Rightarrow \widehat{ABM}=\widehat{ACN}$

Xét tam giác ABM và tam giác ACN có:

$\widehat{ABM}=\widehat{ACN}$

AB = AC (tam giác ABC cân tại A)

BM = CN (gt)

$\begin{align} & \Rightarrow \Delta ABM=\Delta ACN\left( c-g-c \right) \\ & \Rightarrow AM=AN \\ \end{align}$

Vậy tam giác AMN cân tại A.

b + c. Ta có: $\Delta ABM=\Delta ACN\Rightarrow \widehat{HAB}=\widehat{KAC}$

Xét tam giác AHB vuông tại H và tam giác AKC vuông tại K có:

AB = AC

$\begin{align} & \widehat{HAB}=\widehat{KAC} \\ & \Rightarrow \Delta AHB=\Delta AKC\left( ch-gn \right) \\ & \Rightarrow HB=CK \\ & \Rightarrow AH=AK \\ \end{align}$

d. Ta có: $\Delta AHB=\Delta AKC\Rightarrow \widehat{HBA}=\widehat{KCA}$

Ta lại có: $\widehat{ABM}=\widehat{ACN}\Rightarrow \widehat{HBM}=\widehat{KCN}\Rightarrow \widehat{OBC}=\widehat{OCB}$

Vậy tam giác OBC là tam giác cân đỉnh O.

e. Ta có: $\widehat{BAC}={{60}^{0}}$ mà tam giác ABC cân nên tam giác ABC là tam giác đều

$\Rightarrow \left\{ \begin{matrix} AB=BC=CA \\ \widehat{ABC}=\widehat{ACB}=\widehat{BAC}={{60}^{0}} \\ \end{matrix} \right.$

Ta lại có BM = BC = CN

$\Rightarrow AB=BC=CA=BM=BC=CN$

Suy ra tam giác MAB cân tại B và tam giác CAN cân tại C.

$\Rightarrow \left\{ \begin{matrix} \widehat{BMA}=\widehat{MAB}=\dfrac{\widehat{ABC}}{2}={{30}^{0}} \\ \widehat{CAN}=\widehat{CNA}=\dfrac{\widehat{ACB}}{2}={{30}^{0}} \\ \end{matrix} \right.$ (tính chất góc ngoài tam giác)

$\Rightarrow \widehat{AMN}=\widehat{ANM}={{30}^{0}}$

$\Rightarrow \widehat{MAN}={{60}^{0}}+{{30}^{0}}+{{30}^{0}}={{120}^{0}}$

Xét tam giác MBH có: $\widehat{MHB}+\widehat{HBM}+\widehat{BMH}={{180}^{0}}\Rightarrow \widehat{HBM}={{180}^{0}}-{{90}^{0}}-{{30}^{0}}={{60}^{0}}$

$\Rightarrow \widehat{HBM}=\widehat{CBO}={{60}^{0}}$

Mà tam giác OBC cân tại O

Suy ra OBC đều.

-----------------------------------------------------

Trên đây là lời giải chi tiết Bài tập 70 trang 141 SGK Toán 7 tập 1 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2 Tam giác Toán 7 Tập 1. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 7. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!